Donner la représentation graphique de la dérivée d'une fonction

Bonjour tout le monde, j'ai besoin de votre aide à propos d'un exercice de math sur les fonctions dérivées & tangente.

Voilà l'énoncé :

La courbe C donnée ci-après est la représentation graphique d'une fonction f définie et dérivable sur [-3;3], dans un repère orthogonal (O, $i⃗\vec{i}$ , $j⃗\vec{j}$ ). Cette courbe vérifie les quatre conditions suivantes :

Elle passe par l'origine O du repère,
Elle passe par le point A (-3;9),
Elle admet au point B d'abscisse 1 une tangente horizontale,
Elle admet la droite (OA) pour tangente en O.

Quel est le coefficient directeur de (OA) ?
L'un des trois schémas numérotés 1,2 et 3 ( donnés ci-après ) est la représentation graphique de la fonction dérivée de f' de f. Indiquer le numéro de ce schéma en précisant les raisons de votre choix.
On suppose que f est définie sur [-3;3] par :

f(x) = ax³ + bx² + cx + d où a,b,c,d sont des nombres réels

a. En exploitant les quatre conditions sur C, montrer que :

a = $13\frac{1}{3}$ ; b = 1 ; c = -3 ; d = 0

b. On désigne par f' la fonction dérivée de f. Factoriser f'(x) et en déduire le sens de variations de la fonction f sur [-3;3].
4.Démontrer que l'équation f(x) = 0 a une unique solution $α\alpha$ dans l'intervalle [1;2] et donner l'arrondi à une décimale de $α\alpha$ .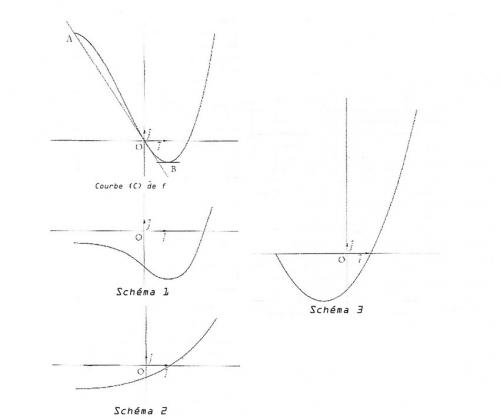

$fichier math$

Donc j'ai fais ça pour l'instant ;

(yO - yA) / (xO - xA)
= (0 - 9) / (0 - (-3))
= -9/3
= -3

Donc le coefficient directeur de (OA) = -3

Je pense que c'est le schéma n°2 ou 3 qui représente la fonction dérivée de f.. Mais je sais pas trop lequel est le bon.

3.a) Je bloque totalement. Une piste pourrais peut-être m'aider.
3.b) Pour la factorisation, j'ai fais comme ça :

f(x)= $13\frac{1}{3}$ x³+x²-3x
f'(x)=x²+2x-3=(x-1)(x+3)

Mais je vois pas comment faire pour la suite de la question.

Je bloque aussi.

Bonsoir,

A partir des variations de f indique le signe de la dérivée.
3)Ecris un système à partir des quatre conditions sur f.
fais un tableau de signes pour la dérivée.

Bonsoir Noémie,

2)Le signe de la dérivée est négative si je ne me trompe pas. Donc ca serai le schéma 2? Mais qu'entends tu par " les variations de f " ?

Je ne vois pas comment écrire un système d'équations avec les conditions données.

Pour le tableau de signe, déjà la fonction est croissante si je ne me trompe pas. Et le tableau sera
-∞ (x-1)(x+3) +∞

Pour les variations de f :
La fonction est décroissante puis croissante, donc la dérivée est négative puis ......

Première condition, la courbe passe par l'origine du repère :
donc si x = 0, y = 0, soit f(0 = 0 + 0 + 0 + d = 0, donc d = 0
deuxième condition, la courbe passe par le point A
....

Pour le tableau de signes :
x - 3 1 3
f'(x) 0 - 0 +

Donc la dérivée est négative puis positive.. Donc le schéma n°2 correspondrai a la représentation?

La courbe passe par le point A
Donc si x = -3 ; y = 9, soit f(-3)=9

Mais comment faire pour écrire l'équation?

Je bloque vraiment sur cet exo

oui schéma 2

Si x = 3, f(3) = 27a + 9b + 3c = 9
Soit 9a + 3b + c = 3
Condition 3
....

Condition 3

Elle admet au point B d'abscisse 1 une tangente horizontale,
Une dérivée de tangente horizontale s'annule en ce point il me semble?

Donc f'(0) = -3
f'(0)=c
c=-3

?

Non,

c'est f'(1) = 0
Calcule la dérivée :
f'(x) = ....
puis f'(1)

f'(1)=0
===> 3a+2b+c=0

f'(x)=x²+2x-3

Oui, 3a + 2b + c = 0

tu ne peux pas utiliser le résultat donné à la question 3 b).

condition 4
...

Je ne vois pas pourquoi calculer la dérivée de f(x) pour cette question?

Sinon la condition 4

f'(-3)=-3
===> 27a-6b+c=-3

L'équation pour la condition 4 est juste.
résous le système d'inconnues a, b et c.

$\left{ {9a + 3b + c = 3 \ 3a+2b+c=0 \ 27a-6b+c=-3} \right.$

Je n'ai pas encore résolu & vu un systéme avec 3 équations et 3 inconnus.
Comment faire ?

Je le verrais peut-être plus tard dans l'année scolaire^^

Deux erreurs,

Condition 2
C'est f(-3) = 9 et non f(3)
Condition 4
la droite (OA) est tangente en O

Ca change quelque chose ?

Oui,

deux équations sont fausses

f(-3) = -27a + 9b - 3c = 9
et
f'(0) = c = -3

Il reste à résoudre :
-3a + b = 0
3a + 2b = 3

f(-3)=9 ===> -27a+9b-3c=9 OK

f'(-3)=-3 ===> 27a-6b+c=-3 Fausse. Je trouve pas

f'(1)=0 ===> 3a+2b+c=0 OK

Ce n'est pas f'(-3) = -3, mais f'(0) = -3

Pas vu tes réponses ^^

Donc on a c = -3 & d=0

-3a + b = 0
3a + 2b = 3

-3a+3a +b+2b =3
3b = 3
b=1

Mais le a=1/3, il est pas là lui >.<

Si
b = 1 et
-3a + b = 0
3a = b
3a = 1
a = ....

Ah oui exactement..
a = 1/3

Merci.

Donc, pour la factorisation ensuite c'est ça
f'(x)=x²+2x-3=(x-1)(x+3)

Pour le tableau de signes :
x - 3 1 3
f'(x) 0 - 0 +
comme tu as dis avant,
ce qui veut dire que la fonction f est croissante sur [-3;3]

Non,

la fonction est décroissante sur [-3;1], puis croissante sur [1;3]

Bonne nuit.

Ah oui c'est pour la fonction f et non pas pour la dérivée..

Bonne nuit, je repasserais demain aux alentours de 20h pour tenté de résoudre la dernière question.

Bonsoir, j'ai réfléchis pour la question 4, mais je ne vois pas vraiment comment faire ?

Sur l'intervalle [1;2], comment varie la fonction ?

Elle est décroissante puis croissante ?

Ah non mince, elle est seulement croissante.

Oui croissante et f(x) varie de ..... à .....
donc ...

f(x) varie de 1 à 2?

Non,

si x varie de 1 à 2, f(x) varie de ...... à ......