aire d'un traingle divisé en 4...
-
Ppyrite dernière édition par
re bonjour,
exercice bonus sensé être logique ....après 2heures passées dessus voilà ce que ça donne....
Le triangle ci dessous est partagé en 4. Trois aires ont des surfaces de 3,7,et 7cm². quelle est la surface de la 4eme ?
( il s'agit d'un triangle quelqueconque , aire du bas à gauche représente un triangle de 3cm², à droite 7cm² et celui d'en dessous 7cm²; en fait il manque l'aire qui fait un losange au dessus )
J'ai essayé en appliquant la loi du chevron; ou le rapport des aires ABM at ACM , avec M le point d'intersection à l'intérieur du triangle, égal à BA'/A'C mais je n'ai aucune longueur.
j'ai essayé en appliquent le théorème de thales mais cela ne me donne rien non plus....
Aire de ABM= 7+x
Aire de ACM= 3+y
mais n'ayant aucune donné...merci de m'aider

-
Bonjour,
Difficile de proposer des pistes sans la figure.
-
Ppyrite dernière édition par
-
Ppyrite dernière édition par
mon exo ne motive personne ??
-
Iiznogoud dernière édition par
Bonjour,
J'ai placé les points suivants sur ta figure :
- A et C les sommets du bas du grand triangle
- O le sommet du haut
- M le point du milieu du triangle
- B l' intersection de CM avec AO
- D l'intersection de AM avec CO
Les points sont placés de telle sorte que l'aire de ABM = 7, celle de AMC = 7 et celle de CMD = 3
Voici les principales étapes de la résolution , que je propose.
J'espère en pas avoir fait d'erreurs.
0. On pose AM = p- Montrer que BM = CM
- Montrer que MD = 3/7 p
- Tracer la parallèle (D1) à AD et passant par B et la parallèle (D2) à OC et passant par B
- Soit B1 l'intersection de (D1) avec OC et B2 l'intersection de (D2) avec AD
- Calculer l'aire du quadralatère B M D D1. Monter qu'elle est égale à 3 fois l'aire de MDC et donc à 9
- Montrer que BB1 = 6/7 p
- Montrer que A B2 = 4/7 p
- En déduire l'aire de B B1 O n indiquant que le triangle B B1 O est homothétique deu triangle B B2 A ==> Aire de B B1 O = 9
- Aire de ce qui est recherché = Aire de B B1 O + aire du quadrilatère de la question 5 ==> solution = 18
Iznogoud
-
Iiznogoud dernière édition par
[
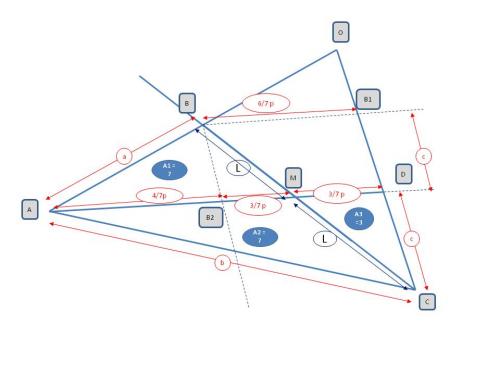
Avec une image, c'est mieux.
Iznogoud
-
Ppyrite dernière édition par
merci beaucoup pour ta réponse, j'essaie d'étudier tout ça et de suivre ton raisonnement ...
