Dire si des surfaces peuvent être de même aire.

Bonjour, j'ai un devoir maison à faire pour la rentrée, j'ai déjà fait les autres exercices mais je bloque sur celui-ci, je n'arrive pas à le démarrer.

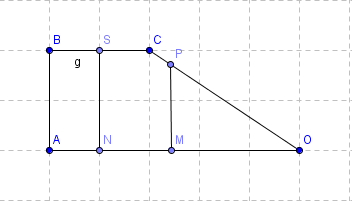
"OABC est un trapèze rectangle de bases OA=4 cm et BC=1.5 cm et de hauteur AB=2 cm
Ce trapèze est divisé en trois surfaces : le triangle rectangle OPM, le pentagone PMNSC et le rectangle NSBA.

Ces trois surfaces peuvent-elles être de même aire ?
Préciser alors les positions de M et de N sur le segment [OA]."

Je me suis dit qu'il fallait que je prenne une inconnue x sauf que je sais pas ou la mettre et qu'il fallait aussi que je trouve les formules des aires des trois surfaces et à l'aide de ma calculatrice j'aurais su si elles pouvaient être de même aire et en quelle aire.

Et la je bloque.

Merci d'avance

Figure de l'exercice

Bonjour,

Vérifie les noms des points sur ton graphique.

Tu demandes de préciser la position des points M et N...

Bizarre car sur ton graphique M est fixe...( Projeté de C sur (AB )

Oui il y a un problème en effet dans les points !
je vais refaire le dessin

Le point M était mal placé ! Mais je sais pas par ou commencer pour démarrer l’exercice ....

Personne peut m'aider s'il vous plait ?

Quelques pistes,

Une inconnue ne te suffira pas vu que tu as deux points variables ; il te faudra deux inconnues : par exemple AN=x et OM=y

Tu peux calculer l'aire du trapère AOCB

$\text{aire(AOCB)=\frac{AO+ BC}{2}\times AB$

Tu dois trouver 5.5 cm²

Les 3 surfaces seront de même aire lorsque chacune des 3 aires vaudra $\text{ \frac{5,5}{3}$cm²

Pour trouver x ( d'où la position de N ) , tu auras :

$\text{aire(ANSB)=\frac{5,5}{3}$cm²

Pour trouver y( d'où la position de M ) , tu auras :

$\text{aire(MOP)=\frac{5,5}{3}$cm²

Merci beaucoup, mais je ne vois pas avec quelle formule je peux trouver x grâce a l'aire ...

Pour x:

$\text{Aire(ANSB)=AN \times\ AB = 2x$

$\text{2x=\frac{5.5}{3} donc x=...$

Donc x=0.9 cm ! Merci maintenant pour y il faut que je fasse $Aire(OMP)=y×1÷2×PMAire(OMP)=y\times 1\div2\times PM$ mais il me manque la mesure PM ...

Tu dois calculer PM en fonction de y.

En appelant F le projeté de C sur (AO) , pense que les triangles OPM et OCF sont semblables ( ou si tu préfères , applique le théorème de Thalès aux triangles )

Ok merci !

Désolé mais je bloque encore, j'ai trouvé le segment [CO] qui est égal à 3.2 cm.

Et la je comptais utiliser le théorème de thalès que [OP] était égal à $y÷sin⁡51.3y\div \sin 51.3$ et donc avec le théorème de Thalès cela aurait donné $(y÷sin⁡51.3)÷3.2=y÷2.5=PM÷2(y\div \sin 51.3)\div 3.2 = y\div 2.5=PM\div 2$ et là je vois pas comment faire ...

Bonsoir,

Indique les rapports pour la propriété de Thalès puis exprime PM en fonction de y.

Bonsoir Moemi et Aetruion ,

Un coup de pouce de plus ,

$\text{\frac{OM}{OF}=\frac{MP}{FC}$

d'où ...............................

y/2.5=PM/2 donc la je fais y=(PM/2)*2.5 ou PM=(y/2.5)*2 ?

Oui.

Tu peux simplifier un peu : PM = 0.8y

Maintenant je vois pas comment faire pour arriver à MO....

Comme déjà indiqué , MO=y

oui mais quel est le rapport entre OM et PM ? j'utilise quelle formule ?

S'il te plait , relis les réponses précédentes.

Il faut que j'utilise le théorème de thalès ....

$y÷2.5=0.8y÷2y\div 2.5 = 0.8y\div 2$ c'est bien cela ?

$\text{Aire(OMP)=\frac{OM\times MP}{2}=\frac{y \times 0.8y}{2}$

Cette aire doit valoir $\text{\frac{5.5}{3}$

Tu dois pouvoir terminer.

Ok merci beaucoup !