Angle inscrits

Bonjour à tous!
J'ai quelques problèmes
La figure: Un cerle (C) ayant pour centre O et pour rayon R
A , B, M appartiennent à (C)
l'angle AMB= 30°
le segment [NB] est un diamètre du cercle (C )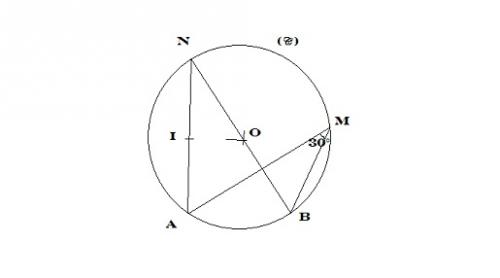 $fichier math$
1- Soit I le milieu , du segment [AN], montrer que les droites (OI) et (IN) sont perpendiculaires.
2-a) Montrer que AB=2Rsin30°
2-b) On admet que sin 30°=1/2
et il faut exprimer la longueur AN en fonction de R
Merci d'avance.

Bonsoir,

Indique tes éléments de réponse et la question qui te pose problème.

Quelle est la nature du triangle NAB ?
Que peut-on dire des droites (OI) et (AB) ?
Utilise la trigonométrie dans le triangle NAB.

La question 1, NAB, rectangle en A, (OI) et (AB) parallèles, si deux droites sont parallèles, et qu'une troisième droite est perpendiculaire a l'une alors elle est perpendiculaire a l'autre.
Donc (OI) est perpendiculaire (IN).
C'est ça ?

Et les questions 2) a. et 2) b. j'y arrive vraiment pas.
Je pense qu'elles se suivent mais comme je ne comprend pas vraiment la 2) a. je n'y arrive pas.

Pour la question 1, il faut justifier
pourquoi le triangle NAB est rectangle (Cite la propriété)
pourquoi les droites (OI) et (AB) sont parallèles (Droite des milieux ?)

Quelle est la mesure de l'angle NAB, justifie la réponse.
Puis
Que vaut sin ANB ?

NAB rectangle: si un triangle est inscrit dans un cercle et que son plus grand coté est un diamètre alors il est rectangle.
(OI) et (AB) sont parallèle: je ne sais pas justifier.

NAB=30 degrés: l'angle AMB mesure 30 degrés et il intercepte le même arc que NAB, leurs mesures sont donc égales ( angles inscrits )
Sin ANB= Sin AMB= Sin 30 degrés.
Mais après, je sais pas.

O est le milieu du segment [NB] et I est le milieu du segment [NI]
donc ...

Dans le triangle NAB, écris la relation sin ANB = AB/...
soit AB = ....

Pour la question deux, je crois que c'est: Sinus 30 = AB/BN or BN= 2R d'ou AB= 2R sin 30, c'est ça ?
Et pour la question 1, je ne connais pas cette propriété ..
Mais merci de m'orienter vers ces réponses, cela m'aide beaucoup

Pour la question 1, je crois que j'ai autre chose:
Comme o est le centre de C et I est le milieu du segment AN alors que la droite IO est la médiatrice du segment AN. Or, une médiatrice est toujours perpendiculaire au segment qu'elle coupe en son milieu. Donc OI est perpendiculaire a IN et comme I est un point de AN alors OI perpendiculaire a AN.
Ça marche ?

Question 2 a) juste.
Question 1
tu ne connais pas la propriété des milieux (4éme) :
Dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté.

Ah oui les souvenirs reviennent
La question trois j'ai peut être quelque chose:
J'en conclus que AB=R
Pythagore: AB²=AN²=BN²=4R² et donc AN= √3R
C'est juste ?

AB=R
Pythagore: AB²+AN²=BN²=4R² et donc AN= √3R

C'est correct

Merci beaucoup pour cette aide !
Mais j'ai cru m'être trompé en écrivant 4R.
Pour 4R en fait ?

BN = 2R
BN² = (2R)² = 2R×2R=4R²

pourquoi 4R ?

Merci beaucoup, je n'avais pas vu la réponse.

Ok, pas de problème.

Bonne nuit

En fait, pourquoi c'est pas √3R au carré ?
Pourquoi il n'y a pas le carré ?

C'est
AN² = 3R²
donc si on prend la racine carré
√(AN²) = √(3R²)
AN = (√3)R
R n'est pas sous le radical.

Ah oui merci beaucoup.