A-t-on sin(2*15°) = 2*sin(15°) ?

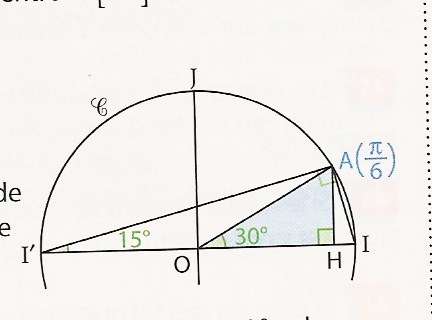
$fichier math$
A est le point image du réel π/6 sur le cercle trigonométrique C de centre O. [AH] est la hauteur du triangle IAI'.

Justifier les mesure 30° et 15° indiquées sur la figure.
a) Montrer que AI' = 2cos15° et en déduire AH en fonction de cos15° et sin15°
b) Déduire une relation simple entre sin 30° et le produit sin15° * cos15°
Répondre à la question posée dans le titre.

Pour la question 1, je pense qu'il faut faire avec les angles au centre etc..

Mais ensuite, je n'arrive pas à faire les 3 questions..

Bonsoir,

Pour AI' utilise la trigonométrie dans le triangle AII'.
puis exprime AH dans le triangle AHI'.

Mais lequel utiliser entre cos, sin et tan ?

Tu dois trouver 2 cos 15°
Donc utilise cosinus.

Donc :

cos = adjacent / hypoténuse

soit : AI' / II' ?

C'est correct.
A quoi est égal II' ?

Ce n'est pas avec : AI'² = II'² + AI ² ?

Non, II' est un diamètre donc II' = ....

II' = 2 * I'O ?

Et I'O = OI = .....
C'est le cercle trigonométrique.

I'O = OI = 1 ?

Oui,

Donc donne le résultat pour AI'.

Donc : cos15 = AI' / II' = AI' / 2 ?
Donc, produit en croix ?

Oui,
donc AI' = ....

AI' = 2cos15

oui.

Exprime AH en fonction de AI' dans le triangle AHI'.

Quel est la formule pour une hauteur ?

Utilise la trigonométrie dans le triangle AHI'.

cos15 = opposé / hypoténuse = AH / AI' = AH / 2
Produit en croix ?
AH = 2cos15 ?

Non,

AH n'est pas le côté adjacent à l'angle de 15°.
C'est le sin15° que tu dois calculer.

sin15 = opposé / hypoténuse = AH / AI' ?
= AH / 2 ?
AH = 2sin15 ?

AI' n'est pas égal à 2.
AH = AI' sin15°
or
AI' = ......
donc
AH = ......

AI' = AO + OI' ?

AH = AI' sin15°
or
AI' = 2 cos 15° (résultat de la question 2)
donc
AH = 2 cos 15 sin 15

Dans le triangle OAH, AH = ....
Donc
....

sin 30 = AH / OA
sin 30 = AH / 1
AH = sin30 ?

Oui
donc sin30° = ....

sin30 = 0.5

A partir de :
AH = 2 cos 15 sin 15
et
AH = sin30°,
tu déduis
sin30° = ......