Valeur exacte de sin 15° et de cos 15°

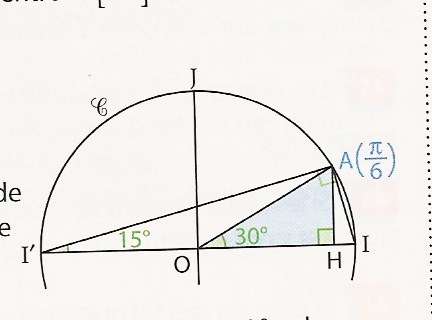
$fichier math$

A est le point image du réel π/6 sur le cercle trigonométrique C de centre O. [AH] est la hauteur du triangle.

Déterminer la valeur exacte de I'H.
a) Exprimer de deux façon cos15°, en se plaçant dans les triangles I'AH et I'AI
b) En déduire que I'H = 2cos²15°
Déduire des questions 1 & 2 la valeur exactement de cos15° Déterminer alors celle de sin15°
Conclure.

Bonsoir,

Indique tes éléments de réponse.
Utilise la trigonométrie dans le triangle OHA.

Donc :

2.a) cos 15° = adjacent/hypoténuse = AH / I'H

Mais comment trouver I'H ?

Complète
Dans le triangle I'AH rectangle en ...
l'hypoténuse est ...
Pour l'angle AI'H,
le côté adjacent est ....
le côté opposé est ....

Dans le triangle I'AH rectangle en H
l'hypoténuse est I'A
Pour l'angle AI'H,
le côté adjacent est I'H
le côté opposé est AH

Ecris le rapport pour cos15°.

cos15 = adjacent / hypoténuse = I'H / I'A ?

Et dans le triangle I'AI ?

cos15 = adjacent / hypoténuse = I'H / I'I ?

Non, H n'est pas un sommet du triangle I'AI.

cos15 = adjacent / hypoténuse = I'A/ I'I

Par contre, j'ai une formule pour calculer Oh et AH

Calcule le produit des deux expressions de cos15°.

Donc : 2cos15 = I'A / I'I * I'H / I'A = I'H / I'I ?

Non
C'est :
cos15 × cos15 = I'A / I'I * I'H / I'A = I'H / I'I
et comme I'I = ....
I'H = ....

Et comme I'I = 2
I'H = 2cos²15 ?

Oui

& donc pour la 3 ?

As tu calculé I'H ?
I'H = I'O + OH
Calcule OH dans le triangle AOH.

OH = x = AH
(OH) ² + (AH) ² = (OA) ²
x ² + x ² = 1 ²
2x² = 1
x² = 1/2
x = 1/√2 * √2/√2 = √2/√2 ?

AH n'est pas égal à x.

A quoi donc alors ?

Exprime AH dans le triangle OAH.
sin30° = ....

sin30 = opposé / hypoténuse = AH / OA = AH / 1
AH = sin30 ?

Oui
et sin30° = ....
Soit
I'H = ....

sin30 = 0.5 ?

(Seulement de passage...je n'ais pas suivi le topic mais si tu veux savoir si sin30=0.5 , je te réponds OUI )

Merci !

Donc la valeur exacte de I'H est ......

I'H = I'O + OH
= 1.9

Non

I'H = I'O + OH
= 1 + cos30°
= 1 + √3/2

et pour la trois ?

C'est une déduction, écris les deux résultats obtenus pour I'H.