Etude d'une fonction carré et problème du second degré
-
AAlexis3010 dernière édition par Hind
Bonjour, est-ce-que vous pouvez m'aider pour un exercice de maths du livre Sym bole maths 2° des éditions Belin ? Exercice 69 page 108. Voilà le sujet :
Une galerie d'arts va bientôt fêter ses 20 ans d'existence. Pour cette occasion, son propriétaire souhaite décorer la pièce principale d'un immense tableau de 4 mètres sur 3. Le peintre chargé de sa réalisation pense que, pour être harmonieux, ce grand tableau devra respecter la condition suivante : l'aire du contour devra être égale à l'aire de la partie peinte. On désigne par x la largeur du contour (en mètre).- Exprimer l'aire du contour de l'aire de la partie peinte à l'aide de la variable x.
- Montrer que la condition proposée par le peintre est réalisée si et seulement si :
2x² - 7x + 3 = 0
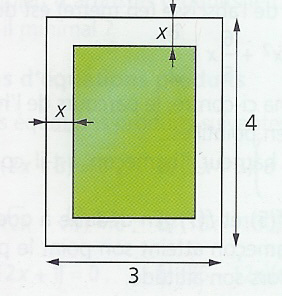
Voilà le schéma pour vous aider.
Merci pour vos réponses.
-
Bonjour,
Indique tes éléments de réponse.
Quelle est l'aire du tableau ?
Quelle sont les dimensions de la partie peinte ?
Quelle est l'aire de la partie peinte ?
-
AAlexis3010 dernière édition par
Noemi
Bonjour,Indique tes éléments de réponse.
Quelle est l'aire du tableau ?
Quelle sont les dimensions de la partie peinte ?
Quelle est l'aire de la partie peinte ?Merci pour ta réponse, mais ce que tu me demandes est justement la première question, j'ai fourni tous les éléments que j'avais.
-
Réponds aux questions :
Quelle est l'aire du tableau ?
Quelle sont les dimensions de la partie peinte ?
longueur :
largeur :
Quelle est l'aire de la partie peinte ?
-
AAlexis3010 dernière édition par
Merci mais je ne trouve pas les réponses. Est-ce-que peux me les donner STP ? Merci
-
Comment calcule t-on l'aire d'un rectangle ?
-
AAlexis3010 dernière édition par
Et bah je fait longueur fois largueur mais là avec les X ça donne quoi ?
-
Les dimensions initiales sont 3 et 4, donc .....
Puis à la longueur 4, on soustrait .....
et à la largeur 3, on soustrait .....
dont aire de la partie peinte ....
-
AAlexis3010 dernière édition par
Est ce que c'est 4-2X fois 3-2X ?
-
Oui,
fais le calcul.
-
AAlexis3010 dernière édition par
L'aire du contour est égale à quoi ? Parce que pour la deuxième question j'ai besoin de l'aire du contour et de l'aire de la partie peinte non ?
-
Pour le contour, tu fais la différence par rapport au rectangle initial et l'aire peinte.
-
AAlexis3010 dernière édition par
Je trouve pour la partie peinte 4X² - 6X + 4 est ce que c'est ça ? Donc pour l'aire du contour je fait: 12 - (4X² -6X + 4) ?
-
Non,
Indique tes calculs.
-
AAlexis3010 dernière édition par
(3 - 2X) * (4 - 2X)
34 - 32X - 2X4 - 2x-2X
12 - 6X - 8 + 4X²
4X² - 6X + 4
-
Un x oublié
(3 - 2x) * (4 - 2x)
34 - 32x - 2x4 - 2x(-2x)
12 - 6x - 8x + 4X²
= ...
-
AAlexis3010 dernière édition par
D'accord merci donc c'est 4X² - 14X +12. Mais pour l'aire du contour je n'ai pas compris comment tu fait
-
L'aire totale 3 x 4 moins l'aire que tu viens de calculer.
-
AAlexis3010 dernière édition par
Je fais 12 - 4X² - 14X +12 ? Ça donne - 4X² - 14X + 24 c'est ça ?
-
Non,
Vérifie les signes.
-
AAlexis3010 dernière édition par
Tu veut pas me donner un indice stp ?
-
12 - (4X² - 14X +12)
= 12 - 4X² + 14X -12
-
AAlexis3010 dernière édition par
Donc l'aire du contour est égal à -4X² + 14X ?
-
Oui, c'est l'expression de l'aire du contour.
-
AAlexis3010 dernière édition par
Et pour montrer que la condition est réalisable que si : 2X² - 7X +3 = 0 je fait comment stp ?
-
Tu écris la relation correspondant à : L'aire du contour = aire de la partie peinte".
-
AAlexis3010 dernière édition par
Donc je fait:
-4X² + 14X = 4X² - 14X + 12
14X = 8X² - 14x + 12
0 = 8X² - 28X + 12Ça ne me donne pas 2X² - 7X + 3 = 0
Comment je fait ? Est ce que j'ai fait une erreur ?
-
Pas d'erreur,
Divise l'équation par 4.
-
AAlexis3010 dernière édition par
D'accord merci beaucoup pour ton aide
-
AAlexis3010 dernière édition par
J' ai une autre question où je n'y arrive pas:
On considère la fonction f, définie pour tout réel X ∈ [0;3] par
f(X)=2X² - 7X + 3.
Représenté graphiquement la fonction f dans un repère orthonormal où en abscisses, 1cm représente 1mètre.Comment je fait pour tracer la courbe stp ?
-
Tu dois connaître l'allure de la courbe.
Détermine les coordonnées de différents points que tu places sur le repère.
-
AAlexis3010 dernière édition par
Je pense qu'il faut d'abord mettre un point a (0;3) mais après je ne sais pas comment je peut faire
-
AAlexis3010 dernière édition par
Est ce que les points sont à (0;3) (1;-2) (2;-3) et (3;0) ?
-
Les coordonnées des points sont correctes.
Il manque le point le plus bas pour x = 7/4.
-
AAlexis3010 dernière édition par
Pour déterminer graphiquement les solutions de l'équation f(X)=0 je fais comment ? Je sais que c'est 0.5 et 3 mais comment je le montre graphiquement ?
-
Tu résous l'équation :
2X² - 7X + 3 = 0
-
AAlexis3010 dernière édition par
Oui mais algébriquement je marque S=[0.5;3] mais graphiquement comment je doit le montrer sur le graphique ?
-
Tu cherches les abscisses des point d'intersection de la courbe avec l'axe des abscisses.
-
AAlexis3010 dernière édition par
D'accord merci. Donc pour trouver quelle largueur de X le peintre devra-t-il choisir pour le contour c'est quoi ? 0.5, 3 ou un autre nombre ? Parce que j'ai fait 4X² - 14X +12 en remplaçant par 0.5 et 3 et -4X² + 14X en remplaçant aussi par 0.5 et 3 mais je ne trouve pas le même chiffre est ce qu'il fallait faire ça ?
-
La valeur pour que le tableau soit harmonieux est x = 0,5 car x doit être < 3/2.