aire maximum

Bonsoir, je me permets de vous exposer mon problème car je n' ai trouvé personne autour de moi capable de le résoudre. Je dois faire cet exercice pourlundi 12 septembre. Merci à ceux qui me liront et m'aideront !

énoncé

ABC est un triangle rectangle en A tel que AB = 1 et AC = 2. P est un point de [AC], Q un point de [AB] et M un point de [BC] tels que APMQ soit un rectangle.

Comment choisir M pour que l'aire APMQ soit maximum ?

mon raisonnement
J'ai donc commencé l'exercice en faisant une figure, pas à l'échelle cependant. J'ai pris 4 cm de côté pour AB et 8 pour AC. (x4 donc pour chacun).
J'ai réussi a obtenir 2 rectangles dedans d'une aire maximum de 30. Les autres aires de rectangles étaient tous plus petites. (30/4 = 7,5 d'aire donc).

Je ne comprends donc pas la question, comment choisir M ? Pouvez vous m'aider ? Si vous ne voyez pas ce que je veux dire, je vous scanne l'exercice ainsi que ce que j'ai fais.

Merci de votre aide.

Bonsoir,

Pose x la largeur du rectangle, ensuite
exprime la longueur en fonction de x.
Puis l'aire du rectangle,
puis recherche le maximum.

J'ai trouvé que, pour que l'aire soit au maximum, tous les points doivent être au milieu de chaque côté.

Je ne comprends pas bien ce que tu veux dire, si je pose x la largeur, cela me donne donc x. La longueur, 0,5x. Je fais x2 pour enlever la virgule, cela me donne :
largeur : 2x
longueur : x

largeur x longueur = 2x²

et après? en fait je ne sais pas comment prouver que lorsque tous les points sont au milieu de leur segment respectif, cela donne l'aire maximum

Salut

En posant AQ = PM = x (on aurait pu faire un autre choix...)

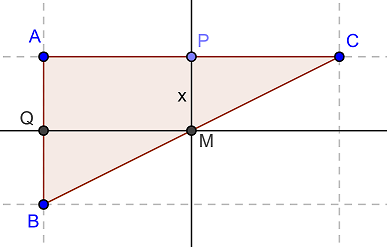
$fichier math$

Exprime AP en fonction de x (Thalès sans doute...) - attention ce n'est pas nécessairement 2x !

Ensuite tu auras l'expression de l'aire de APMQ en fonction de x, dont il te faudra chercher le maximum.