Calcul de la tangente d'un angle

Bonjour à tous !

Ce midi je me suis lancé dans mon petit DM de Maths. Qui c'est avéré.. Coriace pour moi.. x)
Bref, voici l'énoncé :

"On souhaite poser les panneaux solaires sur un toit qui a la forme d'un trapèze rectangle représenté ci dessous par le quadrilatère ABCD. Les panneaux solaires occuperaient le rectangle MAPN."

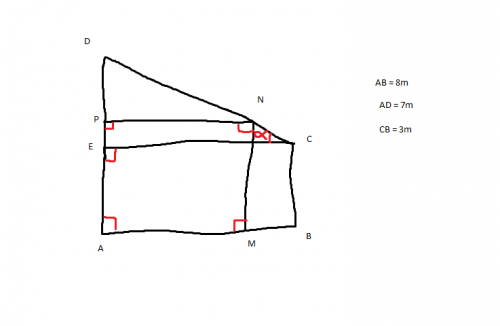
DM Maths énoncé

"* On note h la longeur AP en m et A(h) l'aire du rectangle MAPN en m²* "

1. Calculer tan Alpha

Bon pour ça. Pas de problèmes. J'ai utilisé Pythagore, etc et j'ai trouver Tan Alpha = (√5)/5

Après..

**2.**En déduire que PN = 14 -2h Et là... J'ai beau chercher, avec l'aide de mon père également je n'ai pu trouver..
Je sais que ED = 4 cm et AE = 3 cm .. Après..
Il doit surement y avoir un rapport avec un tangente calculer précédemment, avec l'angle ECD et PND.

Avez vous des pistes, conseils s'il vous plait ? Merci !

(Suite de l'exercice)

3. Exprimer l'aire A(h) du rectangle MAPN en fonction de h. Préciser l'ensemble de ddéfinition de la fonction A.

4. Comment doit etre h pour que A(h) ≥ 24 m² ?

5. Dresser le tableau de variation de A et donenr l'aire maximale de MAPN.

Voilà. Pour l'instant je n'ai pas fait attention à l'autre partie. J'essais surtout de résoudre la b. avant.

Merci d'avance !

Bonjour,

Pourquoi Pythagore pour tan alpha ?
Indique tes calculs.

A quoi correspond h ?

J'avais besoin de connaitre DC. Valeur inconnue. Et pour calculé la tangente. C'est l'opposé divisé par l'hypoténuse.

DC² =DE² + EC²
DC² = 4 ² + 8²
DC² = 80
DC = 4√5

Tan Alpha = O/H = 4/ 4√5 = √5/5

h correspond à AP.

Non,

La tangente est égale au rapport du côté opposé sur le côté adjacent.

Ha oui mince.. :frowning2:

Merci ! Je rectifie sa tout de suite !

Donc la tangente serait égale à 1/2.

Auriez vous une piste ou un conseil pour la b. s'il vous plait ? Merci.

Oui 1/2

Merci pour m'avoir dit pour la tangente..

Pour la suite, analyse la figure.

Hmmm... Peut il y avoir un rapport avec le triangle DPN ?
Sachant que l'on connait Tan Alpha..

J'allais dire, PNMA est un carré. Mais il n'y a aucune indication le précisant.. Il est dit aussi que c'est un rectangle.

Si CB = 3 m alors EA = 3m puisque CB = EA .
DE est donc égale à 4 m.

Je continue à réfléchir..

Si tu compares les triangles DPN et DEC , ......

Ils sont proportionnels..
J'en sais rien.. Je suis en train de m'embrouiller pour rien.. Je cherche compliquer alors qu'à mon avis sa doit être simple.

OUI. Sa y est je vois. Sa vient de me revenir, mais sa remonte à loin.. :frowning2:
Il y a un propriété avec les triangles. Du fait que PN et EC soit parallèles.. Arg.. Je vais chercher la leçon sur le net.

Les triangles sont semblables, donc l'angle DNP = l'angle DCE
donc exprime la tangente de l'angle DNP.

Ce que j'ai fais tout à l'heure. Mais sa donne DP/PN et je n'ai pas DP.

Mais je pense avoir trouver. Vit à vit de PN et EC. Il y a une propriété qui en parle mais sa fait 2/3 ans que je ne l'ai pas vu.. PN et EC sont parallèles et appartienne au triangle DEC. Sachant que EC = 8m, DE = 4 m, DC = 4√5 m

AD = 7 et AP = h, donc DP = ....

Donc DP = 7 - h

Oui, c'est juste.

J'ai tenter DP/DE = EC/PN. Suis je sur la bonne voie ?

Cul de sac... PN ( 7-h ) = 32 ..

Utilise tan DNP = 1/2
soit ....

Mais oui ! Je fais le calcul..

C'était tout bête.. Aïe..
Merci beaucoup je retrouve bien le résultat !

tan Alpha ' = DP/PN
1/2 = (7-4)/PN
PN = 2(7-h)
PN = 14 - 2h

3. A(h) = L x l
= h(14 -2h)
= 2h² -14h

Ensemble définie sur .. ℜ ?

Pour que A(h) ≥24

2h² - 14h - 24

Delta = b² -4ac
= 14² - 4 x 2 x (-24)
= 196 +192
= 388

Donc deux solutions :

x1 = (-7 + √94)/2
x2 = (-7 + √94)/2

Je trouve cela bizarre ..

Attention aux signes
A(h) = L x l
= h(14 -2h)
= -2h² +14h

h varie de 0 à AD, donc h appartient à ......

4 Résoudre -2h² + 14h -24 ≥ 0

h varie de 0 à AD, Donc h appartient à ] 0 ; + ∞ [

Résoudre

∇= b² - 4 ac
∇=4

x1= 3
x2= 4

AD = 7, donc h varie de 0 à 7.

Tu as calculé les valeurs qui annulent l'équation, il est demandé l'ensemble des valeurs pour lesquelles l'inéquation est vérifiée.

Arg.. Je me disais pourtant c'est surement avec Delta puisque nous sommes en plein dedans. Je relis l'énoncé. Merci.

Comment pourrais je faire pour trouver h pour que A(h) ≥ 24 m² ? Faire -2h² + 14h ≥ 24 .. Ce n'est pas possible..

Bon. Je vais me coucher. Comme on dit la nuit porte conseil. Merci beaucoup pour ton aide Noemi. Je continuerais sa demain matin. Bonne soirée.

A(h)≥24m² pour tout h supérieur ou égale à 3.

Tu dois résoudre l'inéquation : -2h² + 14h -24 ≥ 0

Factorise l'expression -2h² + 14h - 24, puis fais un tableau de signes.

bonjour, je suis resté bloqué a la premiere question ... je ne comprend pas comment faire . je sais que : tan alpha = DE/EC et apres je bloque mais alors complètement.

Bonjour
Personnellement je suis bloqué au fait de trouver l'ensemble de definition, je n'ai pas tres bien compris comment il fallait s'y prendre

Bonjour Crymos et Loktam,

Des éléments de réponse à vos questions sont dans les premiers posts.

Oui en effet j'avais mal regarder, mais finalement j'y suis arriver.
Mais pour l'inequation, je trouve, dans mon tableau de signe, l'ensemble de definition S= ]-infini;3] U [4;+infini[ mais je ne sais pas si cela est correct, pourriez vous eclairer ma lanterne svp?

C'est l'ensemble solution ou l'ensemble de définition ?

h varie de 0 à 7.

L'ensemble de définition Noemi.
Pour -2h² + 14h -24 ≥ 0
Les solutions sont égales à 3 et à 4.

Pour le tableau de variation de A je suis pas vraiment du même avis que Crymos. Il faudrait plutôt calculer le sommet a ce moment là.

La solution serait donc de -∞ à S (Sommet) décroissante puis de S à + ∞ croissante. Puisque a est négatif.