Géométrie Géogébra Triangles rectangles

Bonjour a tous,

Je dois faire une figure grâce au logiciel Géogébra, voici l'énoncé:

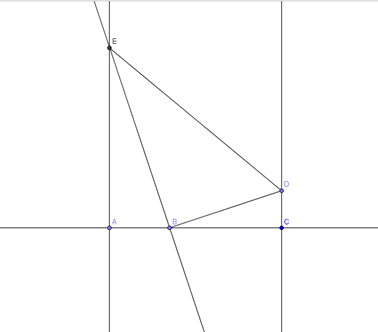
Soient $x$ et $y$ deux nombres strictement positif. BCD est un triangle rectangle en C tel que CD=1, B appartient au segment [AC], ABE est un triangle rectangle en A et EBD est rectangle en B. On pose AB = $x$ , BC = $y$ . I est le point de [AC] tel que AI=1

Faire la figure sur Géogébra en laissant les points A et B libres et E dépendant de A et B (les triangles BCD, ABE et EBD doivent rester rectangles lorsque l'on bouge A et B).

Quand je fais la figure et que je bouge A et B les triangle ne reste pas rectangle.

Merci de votre réponse

Bonjour,

As-tu fixé la mesure de l'angle à 90° ?

Bonjour Noemi,

Non je n'est pas fixé la mesure d'angle à 90° mais voici comment j'ai fait:

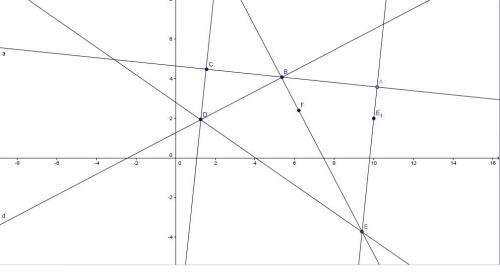
$fichier math$

Quand je bouge mon point B l'ensemble bouge mais pas que je bouge mon point A.

Merci de votre réponse.

Pour la construction, il faut fixer les invariants,
CD = 1, le triangle est rectangle en C, donc le point B appartient à la perpendiculaire à [CD].
.....

Je vois pas comment on fixe CD=1 sur Géogébra.

Merci

Utilise : segment crée par un point et une longueur.

Bonjour,

J'ai refait la figure en fixant les invariants:

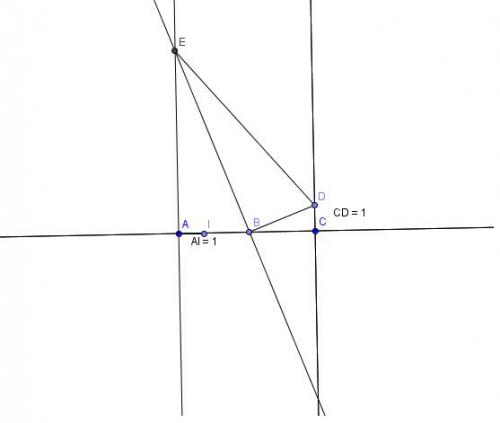
$fichier math$

Est-ce que ça serait comme ça ?

La figure semble correcte.

Fais varier la position des points A et B et vérifie que les triangles BCD, ABE et EBD sont toujours rectangles.

Oui quand je bouge les points A et B l'ensemble des triangles reste rectangle sauf que la mesure de AI et CD change.

Tu as utilisé : segment créé par un point et une longueur.

Non parce-que je sais pas vraiment comment l'utiliser :frowning2:

A partir du point C, tu utilises : segment créer par un point et une longueur que tu fixes à 1.

Quand je bouge le point A sa donne ça:

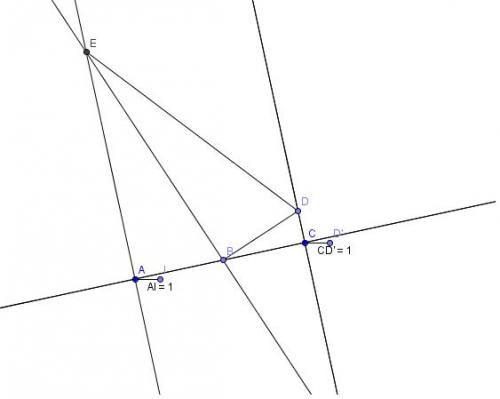
$fichier math$

Le point I doit être sur le segment [AC] et le point D est sur la perpendiculaire à la droite (BC).

Quand je clique sur le point C et que je rentre ma longueur 1 sa me fait ça et pareil pour le pont I.
Je ne sais pas comment mettre le point I sur le segment [AC] et le point D sur la perpendiculaire de la droite (BC)

Tu aurais du créer le segment, puis la droite.

Est-ce que ça serait comme ça ?

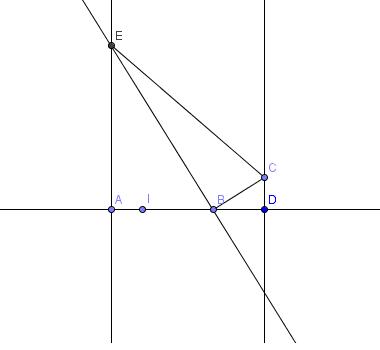
$fichier math$

Quand je bouge le point A il y a que le triangle EAB et EBC qui bouge et quand je bouge le point B il que le triangle EBC et BDC qui bouge est-ce normale ?

Les points C et D sont inversés.

Je les renommes ?

Oui

ok merci beaucoup Noemi, une autre question il faut que j’émette une conjecture sur l'expression de la longueur AE en fonction de $x$ et $y$ .

AB = $x$ ; BC = $y$

Mais je sais pas comment m'y prendre pour émettre cette conjecture.

Repère avec Géogébra les longueurs AE, AB et AC, et fais varier la position des points A et B.

Les longueurs varient quand je bouge les points A et B.

ça serait la conjecture ?

Oui,

mais peut-on trouver une relation entre les trois mesures ?

Une relation comment ça ?

Par exemple AE = AB + BC
ou
....

ED = DB + BA

La question porte sur une relation entre AE et AB et BC non ?

De la longueur AE en fonction de $x$ et $y$

Oui x et y mais x = AB et y = BC.

Compare AE avec AB x BC

AC a la même longueur que AE

Bonjour,

J'aimerais savoir si cela est juste :

$fichier math$

A. Exprimer le plus simplement possible tan $AEB^\widehat{AEB}$

$tan=cote−opposecote−adjacenttan=\frac{cote-oppose}{cote-adjacent}$
$tan=ABEAtan=\frac{AB}{EA}$

B. Exprimer le plus simplement possible tan $CBD^\widehat{CBD}$

$tan=cote−opposecote−adjacenttan=\frac{cote-oppose}{cote-adjacent}$
$tan=CDBCtan=\frac{CD}{BC}$

Merci

Les relations pour les tangentes sont justes.
AC = AE est un cas particulier.

Merci de ta réponse Noemi

Bonsoir,

J'ai encore une question a propos de mon exercice,

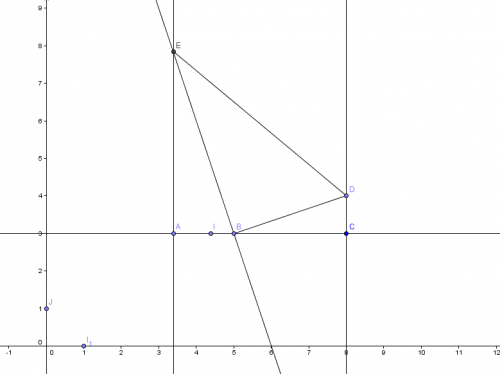
$fichier math$

On se place dans le repère orthonormé (A;I,J). On pose E(0; $e$ ) avec $e$ >0.

A. Sachant que EBD est rectangle en B, déterminer $e$ .

Je ne vois pas du tout comment faire :mad:

Merci beaucoup pour votre aide.

Utilise le fait que les vecteurs EB et BD sont orthogonaux.

Le problème c'est que j'ai jamais vue les vecteurs, comment faut-il s'y prendre ?

Merci

Et la propriété de Pythagore ?

Oui bien-sur je la connais il faut l'appliquer ?

Une question, $e$ c'est la longueur ED qui faut trouver ?

Merci

Non la longueur AD