Généralités sur les fonctions (problème ouvert)

Bonsoir,

Je n'ai aucune piste pour l'exercice suivant qui fait partie d'une des exercices d'un DM de Maths que j'ai à rendre pour la rentrer; merci de me donner des pistes pour pouvoir le faire et le réussir.

Permis de construire
M.La Pioche souhaite construire une petite maison sur son terrain. Les autorités lui imposent un certain nombre de contraintes pour obtenir son permis de construire:
-le-tout-à-l'égout se trouve au point O et le raccordement ne doit pas excéder 15m. M.La Pioche souhaite que cette longueur soit maximale;
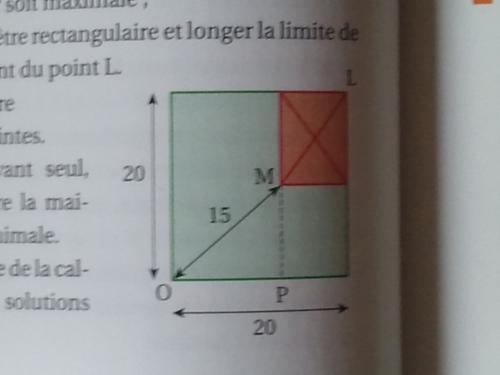
-la maison doit être rectangulaire et longer la limite de propriété en partant du point L.
(il y a un schéma représentant ces contraintes sur un plan).
M.LA PIOCHE, vivant seul, souhaite construire la maison de surface minimale.
Déterminer à l'aide de la calculatrice les deux solutions de son problème.

Merci d'avance pour pour votre aide !

Sans le schéma, dur de répondre et donc d'avancer ...

C'est mieux

Eh bien à la vue du problème , le raccordement OM doit être
exactement = 15 m

car sinon s'il est plus court alors la surface de la maison va devoir
augmenter et comme on veut cette surface minimale ...
(en plus M.La Pioche souhaite que cette longueur soit maximale)

Et si OM > 15 m alors on excède la longueur autorisée ...

Maintenant que sera cette surface ?

on connait l'aire de son terrain 20 X 20

soit x la largeur de la maison, y sa longueur
il faut maintenant compte tenu des renseignements donnés
essayer de trouver x X y ...

Bref il faut réfléchir, alors des idées ?

Il faudrait que l'on calcule la longueur OP pour pouvoir faire 20- ?
Mais il nous manque la longueur MP pour faire un théorème de Pythagore.
Je pense aussi que le raccordement de 15m est une diagonale d'un carré. Carré qui pourrait nous donner quelque chose comme OL(20)- ?
Mais là non plus je ne vois pas comment faire ...

Non j'ai trouvé autre chose:
Si je fais un théorème de Pythagore sur le triangle OMP avec OM=20-y et OP=20-x. Sauf que je me retrouve avec $M P$ ^2 $= 15$ ^2 $20-x)^2$
Et ça me donne quelques chose de négatif. Ou je suis me suis trompé dans les calculs. J'ai des problèmes avec les changements de signes lorsqu'il y a un moins devant une parenthèse ..

Je pense que tu as juste avec Pythagore mais
je cherche aussi de mon coté car si MP=20-y
(attention tu as noté OM=20-y )
alors (20-y)²=15²-(20-x)²
donc on a deux 2 inconnues mais 1 seule équation ... pour l'instant !

Là par contre je ne suis plus trop ... Enfin je ne vois pas comment avancer.

Bonjour loict et messinmaisoui

Une petite aide :
A partir de l'équation : (20-y)²=15²-(20-x)²
isoler y en fonction de x.
ce que l'on cherche c'est l'aire de la maison, Soit A = xy.
Ecrire A(x) et fonction de x, puis utiliser la calculatrice.

Ah Merci Bien Noemi
C'est le genre de problème où on tourne
facilement en rond ...

Donc .. Si j'ai bien compris le membre de gauche $20-y)^2$ doit passer à droite pour former un A(x)=Xy ?!
(Et si c'est ça, je passe le membre de gauche de quelle façon vers la droite ?)

A partir de l'équation :
(20-y)²=15²-(20-x)²
20-y = √[15²-(20-x)²]
y = 20 - ......

Puis l'aire A = x*y
Soit
A(x) = x(20 - ......)
fonction que l'on étudie à l'aide de la calculatrice

Une chose dans l'énoncé m'intrigue quand même
=> "...les deux solutions de son problème ..."

Est-ce que l'énoncé est bien complet, pas d'indice supplémentaire ?

On obtient bien deux solutions pour x. Cela correspond à la permutation possible de x et y.

Le problème là c'est que je me retrouve avec une racine qui fait 5.385164807. Et je suppose que je ne peux pas arrondir .. Donc j'ai un problème de calcul là.

Et .. Je ne comprends pas non plus ce que je dois rechercher dans la calculatrice lorsque j'aurais ma fonction .. (j'ai du mal avec les maths ..).

A la calculatrice, soit avec le tableau de valeur, soit avec le graphique, tu cherches les valeurs de x pour lesquelles la fonction est minimale.

Est-ce que quelqu'un pourrait me reprendre ce qu'il faut que je fasse s'il vous plait, parce que j'ai beau reprendre les étapes, je me perds et je ne comprends pas.. (merci d'avance).

As-tu trouvé la fonction A(x) = ......?

Non étant donné que je suis bloqué avec cette racine où je trouve 5, ..; vu qu'il y a pas mal de chiffres et qu'il faut quelque chose d'exact je me dis que j'ai un problème.

A partir de :
20-y = √[15²-(20-x)²]
y = 20- √[15²-(20-x)²] que tu peux laisser ainsi ou développer le radical.

Soit A(x) = x( 20- √[15²-(20-x)²])
c'est cette fonction que tu programmes à la calculatrice.

Pour x=5 on a 100.

Donc cela veut dire que x=5cm et cela nous donne un aire à 100cm². C'est ça ?
et quelle est la deuxième solution ?

Comment as tu trouvé x = 5 ?

As tu tracé la représentation graphique de la fonction ?
As tu fait un tableau de valeurs ?

J'ai trouvé x=5 en rentrant ma fonction dans la calculatrice; dans le tableau de valeurs, 5 est la plus petite valeur qui apparait (les autres il y a ERREUR).

Fais le calcul pour x = 5, 6, 7, jusqu'à 15.

Ah oui d'accord donc pour x=13 je trouve 87,532, la plus petite valeur du tableau. C'est ça ?

Pour x=14 pardon.

Tu dois trouver deux valeurs pour x.

Prend un pas de 0,5.

Bon, j'ai mon tableau de valeurs avec une colonne x et l'autre colonne Y1 correspondant à A(x); j'ai un pas de 0.5; mais je ne comprend pas quelles valeurs il faut trouver vu qu'il y en a beaucoup. (les deux valeurs les plus petites, .. ? ).

Tu cherches les valeurs de x pour lesquelles Y1 est minimum.

Pour x=6,5 on a 87,501
Et pour x=13.5 on a 87, 5
Ce sont les valeurs les plus basses de Y1

Oui,

Tu as trouvé les deux solutions.

D'accord .. Bai merci encore une fois pour votre aide !