3. étude graphique et algébrique d'une fonction

étude graphique et algébrique d'une fonction

  • C

    Bonjour

    Exercice :

    Soit (Cf) la courbe représentative dans un repère ( O, I, J) d'une fonction f définie sur [-7;3] .

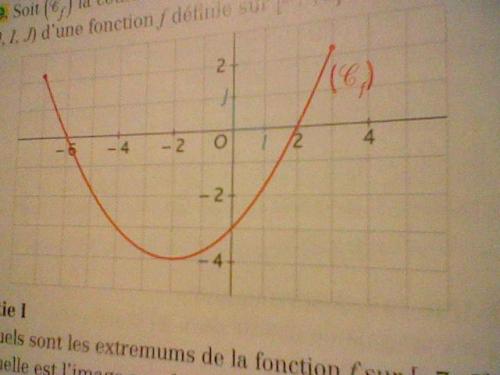
    fichier math

    Partie I

    1. Quels sont les extremums de la fonction f sur [-7; 3] ?
    2. Quelle est l'image par f de 0 ? de -4 ?
    3. Quels sont les éventuels antécédents de -3 ? de -4 ?
    4. Dresser le tableau de variation de la fonction f sur [-7; 3 ] .
    5. Déterminer le signe de la fonction f sur [-7; 3].
    6. Résoudre graphiquement les équations f(x) = 1 et f(x) = 3.
    7. Résoudre graphiquement l'inéquation f(x) > -3 .
    8. Déterminer un encadrement par des nombres entiers des solutions de l'équation f(x) = -2.

    Partie II
    La courbe (Cf) représentée sur le schéma est celle de la fonction f définie sur l'intervalle [-7 ; 3] par :
    f(x) = 1/4x² + x - 3.
    9. Déterminer les images par f de -4 et 0.
    10. Déterminer algébriquement les solutions de l'équation f(x) = -3.
    11. Déterminer algébriquement les solutions de l'équation f(x) = -4.

    Aide : Développer ( 1/2x+1)²

    Voici mes réponses :
    Partie I :

    1. Les extremums de la fonction f sur [-7; 3 ] sont 2,2 et -4. ( je sais pas si je dois expliquer que f admet un maximum 2,2 en ......)

    2. f(0) = -3. Donc l'image par f de 0 est -3.
      f(-4) = -3. Donc l'image par f de -4 est -3.

    3. Les antécédents de -3 sont 0 et -4.
      Les antécédents de -4 sont -2.

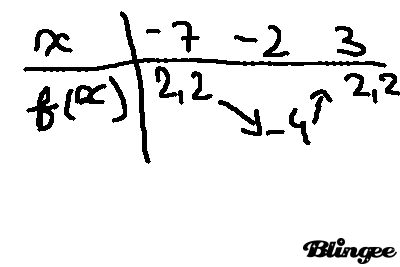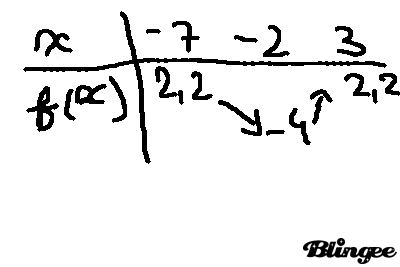
    fichier math

    1. f positive sur [-7 ; -6] U [2; 3]
      f négative sur [-6; 2]
    2. f(x) = 1
      Les solutions de l'équation sont les abscisses des points d'intersection de la courbe représentant f avec la droite d'équation y = 1.
      S = {1,4 ; -5,4}

    f(x) = 3
    Les solutions de l'équation sont les abscisses des points d'intersection de la courbe représentant f avec la droite d'équation y = 3.
    S = 0 ( un 0 barré) IMPOSSIBLE

    1. f(x) > -3
      Les solutions de l'inéquation sont les abscisses des points d'intersection des points de la courbe qui sont au-dessus de la droite d'équation y = -3.
      S = [-7 ; -4] U [3 ; 0 ]

    2. f(x) = -2
      Les solutions de l'équation sont les abscisses des points d'intersection de la courbe représentant f avec la droite d'équation y = -2.
      S = {-4,9 ; 0,9} ( je suis pas sur que c'est ça car ils disent un encadrement...)

    Partie II :

    1. f (x) = 1/4x² + x -3
      f(-4) = 1/4 X -4² + (-4)-3
      f(-4) = - 4 -7 ( ou peut-être c'est : f(x) = 4 - 7 )
      f(-4) = -11

    L'image par f de -4 est -11.

    f (x) = 1/4x² + x -3
    f(0) = 1/4 X 0² + 0 - 3
    f(0) = 0 + (-3)
    f(0) = -3

    L'image par f de 0 est -3.

    1. f(x) = -3
      1/4x² + x - 3 = -3
      1/4x² + x - 3 +3 = -3 + 3
      1/4x² + x = 0
      (1/2x+1)² = 0
      (1/2)² + 2 X 1/2x X 1² = 0
      1/4 + 1x = 0

    Donc les antécédents de -3 sont 1/4x et 1x. (je ne suis pas sur que c'est bon)

    1. f(x) = -4
      1/4x² + x - 3 = -4
      1/4x² + x - 3 + 3 = -4 + 3
      1/4x² + x = -1
      1/4x² + x + 1 = -1 + 1
      1/4x² + x + 1 = 0
      (1/2x + 1)² = 0

    Donc les antécédents de -4 sont 1/2 x et 1. ( je ne suis pas sur que c'est bon )

    Pouvez vous me dire si mes réponses sont bonnes et si j'ai bien rédigé mes réponses s'il vous plait.
    Merci d'avance.

    edit : merci de donner des titres significatifs*

    N 1 réponse
  • N
    Modérateurs

    Bonsoir chat

    Le début est juste.

    1. une inversion [0 ; 3]
    2. Il est demandé un encadrement par des nombres entiers.
    3. f(-4) à vérifier (-4)² = 16
    4. Factorise l'expression 1/4x² + x
    5. Résous l'équation 1/2x + 1 = 0
Se connecter pour répondre