Enclos dimension et aire

Je suis bloquer sur cette exercice, si vous pouviez m'aider sa m'aiderais vraiment.

Voici l’énoncer

Le mur d'une étable a 75m de long. Le propriétaire veut appuyer un enclos rectangulaire contre ce mur. Il dispose de 100m de clôture. On veut déterminer x et y de façon que l'aire A de l'enclos soit la plus grande possible.

Qu'elle est la plus grande valeur que peut prendre x ?
Quelle relation existe-t-il entre les longueurs x et y
Montrer que A(x) = x(100-x) / 2
Résoudre l'équation x (100-x ) = 2500 et l'inéquation x ( 100 - x ) inférieur ou égale à 2500.

Bonsoir,

Indique tes éléments de réponse et la question qui te pose problème.
As tu fait une figure ?

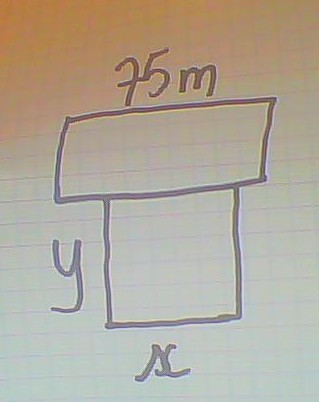
J'ai fais la figure suivante : $fichier math$

Je n'arrive à répondre à aucune questions je suis bloqué, mais pour la questions 1 je pensais que la plus grande valeur était 100m vue qu'il dispose de 100m

Si tu prends x = 100, tu n'obtiens pas un enclos.

Exprime la dimension de la cloture de l'enclos en fonction de x et y.
Puis l'aire de l'enclos en fonction de x et y.

La valeur de x la plus grande est 75 non ? vue que le mur mesure 75m

La dimension de l'enclos je ne sais pas comment faire mais l'aire c'est xy car c'est un rectangle est l'aire d'un rectangle c'est longueurlargeur

Oui,

Comment calcule t-on un périmètre ?

Le périmètre d'un rectangle c'est 2l+2L donc en fonction de x et y sa donne 2x+2y ?

Tu utilises le mur de l'étable, donc .....

Donc, sa donne 75-(2x+2y) ?

Non,

Prends en compte ton schéma.

Sachant que le mur est de 75m la plus grande valeur que peut prendre x est 75 sinon, au dessus de 75 ce n'est plus un enclos ?

Oui,

mais sur ton schéma, tu n'as pas pris le mur en totalité, donc tu ne peux pas utiliser la dimension 75.

Mais c'est comme même 75 la valeur la plus grande ?

Oui la valeur la plus grande possible est 75.

Quelles sont les dimensions de l'enclos ? x et y
donc le périmètre en fonction de x et y est .....
en tenant compte que l'enclos s'appuie contre le mur.

75-2x+2y ?

Non,

Le périmètre est x + 2y.

Donc, la relation qu'il y a entre x et y est x+2y ?

Non,

C'est x + 2y = 100

Pour le calcul de l'aire, exprime y en fonction de x.

Donc pour la question 1 la réponse est que la plus grande valeur que peut prendre x est 75 sinon ce n'est plus un enclos.
Et pour la question 2 la réponse est que la relation entre les longueurs x et y est x + 2y = 100 car pour calculer l'aire, il faut exprimer y en fonction de x ?

Ce n'est pas ça ?

Oui
1 la réponse est que la plus grande valeur que peut prendre x est 75 sinon ce n'est plus un enclos.
Et pour la question 2 la réponse est que la relation entre les longueurs x et y est x + 2y = 100.

Mais comment je peux définir y grace à sa ?
Parce que dans la question trois ils me donnent un tableau et je dois le remplir, mais j'ai seulement la valeur de x

Donne l'énoncé de la question 3.

Si tu as x, tu peux calculer y avec la relation x + 2y = 100.

Compléter le tableau ci-contre :

$fichier math$

Pour trouver y je dois faire une équation non ?
Mais pour trouver A je fais comment ?

J'ai trouver, pour trouver y je fais une équation et pour trouver A je multiplie x*y ?

Comment je pourrais faire pour montrer que A(x) = x(100-x)/2 ?

Pour la formule de l'aire :
Aire = x*y et à partir de la relation 2y + x = 100
tu isoles y = .....
que tu remplaces dans x * y

J'ai trouver et finis l'exercice merci

Tu as résolu l'équation et l'inéquation ?