Calcul des équations de tangentes, variations et représentation graphique

bonsoir,soit f la fonction définie et dérivable sur l'intervalle [ - 1 ; 4]dont la représentation graphique,dans un repère orthonormal (O, $i⃗,j⃗)\vec{i},\vec{j})$
est la courbe c donnée ci- contre.
la droite (T) est la tangente à la courbe au point A.
la droite( T') est la tangente à la courbe au point B.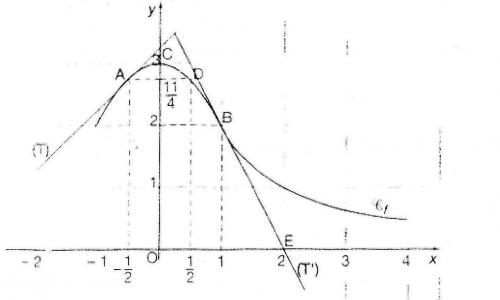 $fichier math$
Et a partir des informations fournies par le graphique
compléter le tableau de valeurs ci-dessous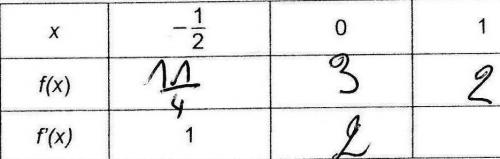 $fichier math$
j'ai commencer mais la derniere colonne je ne vois pas

Calculer une équation de la tangente (T)
Calculer une équation de la tangente (T')
Donner le tableau de variation de f
Résoudre graphiquement dans [-1 ;4] l'équation et l'inéquationsuivantes:
a)f(x)= $114\frac{11}{4}$

b)f(x)≤ $114\frac{11}{4}$

merci de votre aide

je ne vois pas la courbe de la valeur f'(x) pourriez vous me donner un point de repère pour que je comprenne car j'ai bien vue la courbe de la valeur f(x)

Bonsoir lolo59

Pour f'(x) c'est le nombre dérivée, soit le coefficient directeur de la tangente à la courbe au point considéré.
Trace la tangente à la courbe au point C, puis indique son coefficient directeur.

pourrai je avoir un exemple car la je suis perdu et je ne comprend plus pour f'(x)est je ne suis pas tres forte en math

Un exemple :
Pour x = -1/2, point A,
tu choisis un autre point de la tangente, par exemple celui qui est repéré par le trait horizontal en pointillé que je note F.

Tu calcules ensuite le coefficient directeur de la droite
(yA - yF) /(xA - xF) , tu trouves 1.

donc pour f'(x)=0, point C
Le calcul sera le suivant
(yC-yD)/(xC-xD) $114\frac{11}{4}$

Non,

pour x0 = 0, tu dois déterminer f'(0)
tu traces la tangente, elle est horizontale, donc pente nulle?
f'(0) = 0

merci je vois a peu pres mais pour f'(x)=1, point B on trace la tangente Le calcul sera le suivant f'(1)=2

Attention au signe !
(yE - yB) / (xE - xB) = .....

j'ai trouvé (0-2)/(2-1)
-2 /1=-1

mon tableau terminer je peux passer a l'équation de la tangente (T)

Attention
-2/1 = -2 !!

Quelle est la forme de l'équation d'une tangente ?

la forme de l'équation est droite donc on va appliquer la formule suivante
y=Ax+b
la tangente passe par le point A {11}{4}; {1}{2}

Y= $114\frac{11}{4}$ x+b
1=11×4÷4+b
1-11=b
-12=b
y=11x+12

Et la relation :
y = f'(x0)(x-x0) + f(x0) ?

donc si j'ai bien compris ma formule est fausse

La relation y = ax+b est juste, mais le calcul est faux.
Il est plus simple d'utiliser les données du tableau.

y=(o)( $12\frac{1}{2}$ -0)+3
y=3

Non,

Utilise la relation :
y = f'(x0)(x-x0) + f(x0)
si x0 = -1/2 ;
y =

y=1/2

Non,

indique tes calculs.

y=f'(x0)(x-x0) + f(x0)
y=-1/2+3
y=2,5

y = f'(x0)(x-x0) + f(x0)
si x0 = -1/2 ;
y =1(x+1/2) + 11/4
= ....

y=1(1+1/2)+11/4
y= 1+1.5+11/4
y=5.25

Non :
y = f'(x0)(x-x0) + f(x0)
si x0 = -1/2 ;
y =1(x+1/2) + 11/4
y = x + 1/2 + 11/4
y = x + 13/4

donc pour l'équation de la tangente(T)est fini le résultat est
y=x+13/4
excuse moi je me suis trompé
y=3,25

pour l'équation de la tangente(T')
on l'équation suivante y=ax+b
y=f'(x0)(x-x0)+f(x0)
si x0=2
y=1(x+1)+11/4
y=1(2+1)+11/4
y=1+3+11/4
y=3,5

une équation de la tangente est de la forme y = ax+b
La réponse pour T est : y = x + 13/4
pour T' :
y=f'(x0)(x-x0)+f(x0)
si x0=1
y=-2(x-1)+2
y = ....

donc je reprend car mon calcul etait faux
y=f'(x0)(x-x0)+f(x0)
si x0=1
y=-2(x-1)+2
y=-2x+2+2
y=x-2+4
y=x+2

y=f'(x0)(x-x0)+f(x0)
si x0=1
y=-2(x-1)+2
y=-2x+2+2
y=-2x+4

donc pour T' ma reponse est
y=-2x+4

pour mon tableau de variation de f
sur la meme ligne je vois
x -1/2 0 1

f 2.5je ne sais comment faire donc j'explique la fleche monte a 0 j'ai 2.75 puis ma fleche descend a 1 j'ai 2

Pour le tableau de variation,
x varie de -1 à 4 avec une variation en 0
soit
x -1 0 4
f(x) .....

excuse moi la je suis perdu je ne sais plus comment il faut faire
x -1 0 4
f(x) 2 0 0.5

x -1 0 4
f(x) 2 flèche vers le haut 3 puis flèche vers le bas 1/2

merci je peux passer a la question 5 resoudre l'équation

f(x)=11/4 a une solution 0
mais pour f(x)≤ 11/4 je comprend pas meme pour celle du haut car moi est les fonctions c 2 je me débrouille mieux en géométrie

je ne sais pas résoudre graphiquement expliquez moi comment il faut faire merci d'avance

Pour résoudre f(x) = 11/4, cherche les coordonnées des points A et D.

les coordonnées des point A et D sont-1/2;1/2

Donc f(x) = 11/4 si x = -1/2 ou x = 1/2.

Résous f(x) ≤ 11/4 partie de la courbe en dessous de l'équation y = 11/4

donc f(x)≤11/4 si x ]-1/2 ;1/2[