Situation géométrique et approche graphique
-
Lloulou08 dernière édition par
Bonjour à tous,
Pouvez-vous me dire si ce que j'ai fait est juste et pouvez-vous m'expliquer pour ce que j'ai pas compris, merci

SITUATION GÉOMÉTRIQUE:
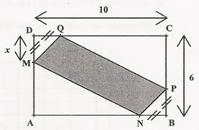
ABCD est un rectangle de longueur AB=10 et de largeur AD=6. On considère le parallélogramme MNPQ inscrit dans ABCD tel que DM = DQ = BN = BP = x.
- Expliquer pourquoi les valeurs de x pour lesquelles la figure est réalisable sont les réels de l'intervalle [0;6].
Je ne comprends pas :frowning2: pouvez-vous m'expliquer.
2.a) Exprimer en fonction de x l'aire du triangle DQM, puis l'aire du triangle QCP.
Aire DQM = base∗hauteur2\frac{base * hauteur}{2}2base∗hauteur
=x∗x2\frac{x*x}{2}2x∗x
=x22\frac{x^2}{2}2x2Et pour l'aire de QCP = base∗hauteur2\frac{base * hauteur}{2}2base∗hauteur
=(10−x)∗(6−x)2\frac{(10-x)*(6-x)}{2}2(10−x)∗(6−x)
=60−16x+x22\frac{60-16x+x^2}{2}260−16x+x2Pouvez-vous me dire si c'est juste, merci :razz:
b) En déduire que l'aire du parallélogramme MNPQ, notée f(x)f(x)f(x) est égale à:
f(x)=60−x2−(6−x)(10−x)f(x)=60-x^2-(6-x)(10-x)f(x)=60−x2−(6−x)(10−x).Aire de DABC = Base∗hauteurBase * hauteurBase∗hauteur
=10∗610*610∗6
=606060Aire DMQ avec PNB =c2c^2c2
=x∗xx*xx∗x
=x2x^2x2Aire de AMN avec PCQ = Base∗hauteurBase * hauteurBase∗hauteur
=(10−x)(6−x)(10-x)(6-x)(10−x)(6−x)donc on en déduis bien que l'aire du parallélogramme MNPQ est f(x)=60−x2−(6−x)(10−x)f(x)=60-x^2-(6-x)(10-x)f(x)=60−x2−(6−x)(10−x)
Pouvez-vous me dire si c'est juste, merci :razz:
c) Démontrer que l'aire de MNPQ est alors donnée par l'expression f(x)=−2x2+16xf(x)=-2x^2+16xf(x)=−2x2+16x.
60−x2−(6−x)(10−x)60-x^2-(6-x)(10-x)60−x2−(6−x)(10−x)
=60−x2−(60−16x+x2)=60-x^2-(60-16x+x^2)=60−x2−(60−16x+x2)
=60−x2−60+16x−x2=60-x^2-60+16x-x^2=60−x2−60+16x−x2
=−2x2+16x=-2x^2+16x=−2x2+16xdonc l'aire de MNPQ est alors donnée par l'expression f(x)=−2x2+16xf(x)=-2x^2+16xf(x)=−2x2+16x.
Pouvez-vous me dire si c'est juste, merci :razz:
- Déterminer par le calcul pour quelles valeurs de x, l'aire de MNPQ est nulle.
Je ne comprends pas :frowning2: pouvez-vous m'expliquer.
- On admet que l'aire maximale de MNPQ est 32. Déterminer par le calcul pour quelle valeur de x, l'aire de MNPQ est maximale.
−2x2+16x=32-2x^2+16x=32−2x2+16x=32
−2x2+4x2=32-2x^2+4x^2=32−2x2+4x2=32
2x2=322x^2=322x2=32
x2=16x^2=16x2=16
x2=42x^2=4^2x2=42
x=4x=4x=4
La valeur x est 4.
Pouvez-vous me dire si c'est juste, merci :razz:
APPROCHE GRAPHIQUE
On donne la courbe de la fonction f qui, à tout réel x de [0;6], associe l'aire MNPQ.
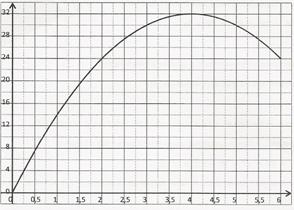
- Déterminer f(1).
L'image de 1 par f est 14.
Pouvez-vous me dire si c'est juste, merci :razz:
- Déterminer les solutions de l'équation f(x)=24f(x)=24f(x)=24.
Les solutions de l'équationf(x)=24f(x)=24f(x)=24 est 2 est 6.
Pouvez-vous me dire si c'est juste, merci :razz:
- Déterminer en justifiant l'aire de MNPQ lorsque M est le milieu de [AD].
Je ne comprends pas :frowning2: pouvez-vous m'expliquer.
Merci.
-
Bonjour loulou08,
- Quelles valeurs peut prendre x ?
- juste.
- Résoudre f(x) = 0
- faux, c'est l'équation du second degré qu'il faut résoudre.
-
Pour l'approche graphique :
- la solution 4 est fausse.
- Si M est au milieu du segment [AD], x = ....
-
Lloulou08 dernière édition par
Bonjour Noemi
- Les valeurs qui peut prendre x sont DQ, BN, BP et DM.
3)−2x2+16x=0-2x^2+16x=0−2x2+16x=0
−2x2+4x2=0-2x^2+4x^2=0−2x2+4x2=0
2x2=02x^2=02x2=0
x2=022x^2=\frac{0}{2}^2x2=202
x=0x=0x=0- J'ai jamais fait de leçons sur le second degrés donc je ne comprend pas.
-
Lloulou08 dernière édition par
Approche graphique:
- Oups désolé j'ai mal vue sur le graphique c'est 6

- Si M est au milieu du segment [AD], x = 6 - x

Merci
- Oups désolé j'ai mal vue sur le graphique c'est 6
-
Pour résoudre l'équation :
-2x² + 16x = 0,
Mets 2x en facteur.Pour résoudre l'équation
-2x²+16x = 32,
-2x²+16x-32 = 0
Mets -2 en facteur et utilise les identités remarquables.AD = 6, si M est au milieu, x = .....
-
Lloulou08 dernière édition par
pour l'équation -2x²+16x=0
2x[2x+16x]=0
2x(18x)=0
36x=0
x=0et pour résoudre -2x²+16x=32
-2x²+16x-32 = 0
Je vois pas comment on peut mettre -2 en facteur.AD = 6, si M est au milieu, x = DQ * DM / 2

Merci
-
Pour résoudre l'équation :
-2x² + 16x = 0,
2x(-x +8)= 0
Et un produit de facteurs est nul si et seulement si ......Pour résoudre l'équation
-2x²+16x = 32,
-2x²+16x-32 = 0
-2(x² - 8x + 16) = 0AD = 6, si M est au milieu, x = 6/2 = ....
-
Lloulou08 dernière édition par
Pour résoudre l'équation -2x² + 16x = 0
2x(-x +8)= 0Un produit de facteurs est nul si et seulement si l'un des deux facteurs est nul

Et résoudre l'équation -2x²+16x = 32
-2x²+16x-32 = 0
-2(x² - 8x + 16) = 0
il faut trouver x après non ?AD = 6, si M est au milieu, x =6/2 = 3
-
Termine la résolution pour la question 3.
x² - 8x + 16 = (x-4)²
-
Lloulou08 dernière édition par
Donc pour l'approche graphique:
- Aire de MNPQ = -2x²+16x
= −2<em>32+16</em>3-2<em>3^2+16</em>3−2<em>32+16</em>3
=−18+48-18+48−18+48
=303030
Merci
- Aire de MNPQ = -2x²+16x
-
Pour x = 3, on détermine graphiquement une aire de 30.
-
Lloulou08 dernière édition par
ok merci noemi je savais pas qu'il fallait le lire sur le graphique.
Pour la situation géométrique
- -2x² + 16x = 0
2x(-x +8)= 0
Si AB = 0 alors A=0 ou B=0
2x=0
x=0et -x+8=0
-x=-8
x=8donc les valeurs de x pour que l'aire de MNPQ soit nulle sont 0 et 8

- -2x² + 16x = 0
-
Non,
x est compris entre 0 et 6, donc la solution est x = ....
-
Lloulou08 dernière édition par
La valeur de x pour que l'aire de MNPQ soit nulle est 0

J'ai mis 8 car l'énoncé dit pour
quelles valeursde x.
-
Non, car x appartient à l'intervalle [0;6] !
-
Lloulou08 dernière édition par
Autrement la valeur de x est bien 0 ?
-
Oui, x = 0.
-
Lloulou08 dernière édition par
Situation géométrique
-2x²+16x = 32
-2x²+16x-32 = 0
-2(x² - 8x + 16) = 0
-2(x-4)² =0
(x-4)²=0
Si X²=0 alors X=0x-4=0
x=4donc la valeur de x est 4.
Est-ce juste ?
-
C'est juste.
-
Lloulou08 dernière édition par
Merci,
Et pour la Situation géométrique le:
- Expliquer pourquoi les valeurs de xxx pour lesquelles la figure est réalisable sont les réels de l'intervalle [0;6].
Les valeurs de xxx pour lesquelles la figure est réalisable sont DQ, BN, BP et DM car ils sont compris dans l'intervalle [0;6].
Est-ce juste ?
Merci
-
x = DM avec M appartenant à [DA], comme DA = 6; x compris dans l'intervalle [0.6]
x = DQ avec Q appartenant à [DC], comme DC = 10 ; x compris dans l'intervalle [0;10]conclusion
x appartient à l'intervalle ...
-
Lloulou08 dernière édition par
x appartient à l'intervalle [0;6]
-
C'est correct.
-
Lloulou08 dernière édition par
Merci
Et une autre question faut le faire pour CB
x=PB avec P appartenant à [CB], comme CB = 6; x compris dans l'intervalle [0.6]

-
Pas utile vu que c'est un rectangle.
-
Lloulou08 dernière édition par
Ok merci beaucoup Noemi pour ton aide.