Devoir Mathématiques géométrie et intervalle
-
Aalexx2b dernière édition par
Bonjour à tous.
Mon professeur de mathématiques m'a donné un devoir à faire pour la rentrée, seulement, je n'ai pas réussi à faire le second exercice, c'est pourquoi je vous demande de bien vouloir m'aider.
Voici l'énoncé :"On veut construire le long d'un batiment une aire de jeu rectangulaire. Celle-ci est entourée par une clôture représentée par le rectangle ABCD avec AB=8m et AD=16m. Une allée de x mètres de large sépare l'aire de jeu de la clôture comme l'indique le croquis ci-dessous :
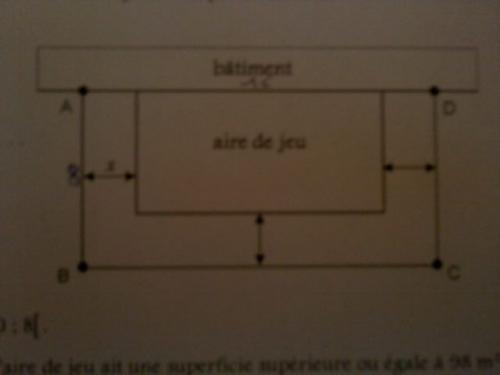
1.Justifier que x ∈ ]0;8[
2.On souhaite que l'aire de jeu ait une superficie superieure ou égale à 98 m².
Quelle doit-être la largeur de l'allée pour qu'il en soit ainsi? "Je souhaiterait que vous m'expliquiez comment justifier le 1 et comment déterminer la largeur de l'allée.
Je vous remercie par avance pour votre aide.
-
Bonjour alexx2b
AB = 8 m donc x peut varier de ....
détermine la longueur et la largeur de l'aire de jeu en fonction de x.
largeur : 8 - x
longueur :
-
Aalexx2b dernière édition par
Si AB = 8m, alors x peut varier de 0 à 8 et on peut donc dire que x ∈ ]0;8[ ?
-largeur : 8 - x
-longueur : 16 - 2xL'air est donc L x l, donc on a (16-2x)(8-x)
--> (16-2x)(8-x) = 98le resultat est x=15 ou x=1 (je l'ai fait à la calculatrice car je n'ai pas reussi a le faire)
Ainsi, lorsque l'on remplace x par 15 ou 1, on obtient 98m².
C'est juste?
-
x ne peut pas être égal à 15 puisqu'il est compris entre 0 et 8.
-
Aalexx2b dernière édition par
oui donc x ∈ ]0;8[ lorsqu'il vaut 1 mais n'y appartient pas lorsqu'il vaut 15.
Une derniere chose, est ce je pourrais avoir la forme développé de l'expression (16-2x)(8-x)=98 ligne par ligne car je n'ai pas reussi?
-
Indique tes calculs pour obtenir une correction.
-
Aalexx2b dernière édition par
(16-2x)(8-x)=98
128-16x-16x+2x²=98
-32x+2x²=-30
x(-32+2x)=-30
-32+2x=-30 ou x=-30
2x=2
x=1
ou alors :
-32x+2x²=-30
2x(-16+x)=-30
2x=-30 ou -16+x=-30
x=-30/2 ou x=-30+16
x=-15 x=-14Voilà à quoi j'ai pensé mais le seul resultat juste est x=1...
-
16-2x)(8-x)=98
128-16x-16x+2x²=98
-32x+2x²=-30
2x² - 32x + 30 = 0
2(x² - 16x + 15) = 0
2[(x-8)² -64 + 15] = 0
2 [ .... ] = 0
-
Aalexx2b dernière édition par
2[(x-8)² -64 + 15] = 0
2[x²-16x+64-64+15]=0
2(x²-16x+15)=0
2(x-15)(x-1)=0
->2=0 impossible
->x-15=0 <=> x=15
->x-1=0 <=> x=1La largeur de l'allée doit donc être de 1m afin que la superficie du couloir soit égale à 98m².
-
C'est correct,
le passage :
2(x²-16x+15)=0
2(x-15)(x-1)=0
est rapide.
-
Aalexx2b dernière édition par
oui je sais mais dans ma tête, je sais comment faire mais je n'arrive pas à le retranscrire
-
Aalexx2b dernière édition par
En tout cas, merci pour votre aide.