Etudier le signe et sens de variation de fonctions
-
Cchat dernière édition par Hind
Bonjour,
Exercice :
On a représenté graphiquement deux fonctions affines f et g.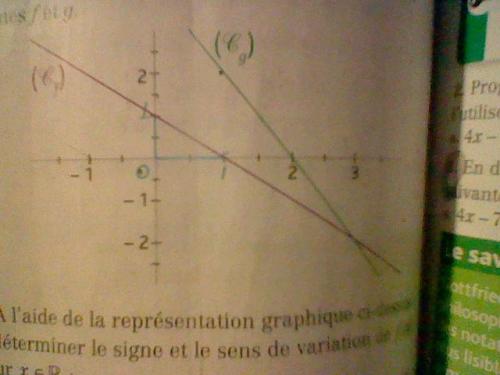
- À l'aide de la représentation graphique ci-dessus :
a. déterminer le signe et le sens de variation de f(x) pour x € (appartient à) R ;
b. déterminer le signe et le sens de variation de g(x) pour x € (appartient à) R. - En déduire les solutions de l'inéquation :
f(x) x g(x) >= 0 ( plus grand ou égal à 0)
Pouvez vous m'aider s'il vous plait car je n'y arrive pas. Merci d'avance.
- À l'aide de la représentation graphique ci-dessus :
-
Bonjour chat,
Indique tes éléments de réponse et la question qui te pose problème.
-
Cchat dernière édition par
Voici mes réponses :
- a.
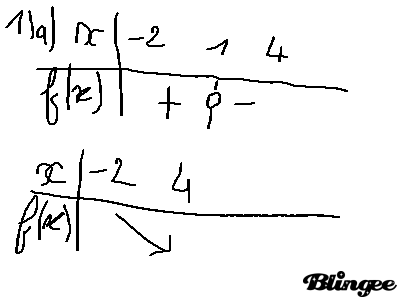
1)b.
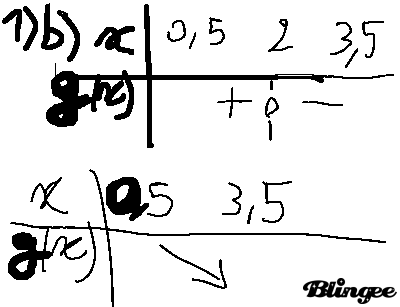
- Je ne sais pas comment calculer
Pouvez vous me dire si mes réponses sont bonnes s'il vous plait et pouvez vous m'aider pour le 2). Merci d'avance.
-
Les deux fonctions ne sont pas décroissantes.
C'est laquelle qui est en vert f ou g ?
-
Cchat dernière édition par
C'est (Cg) qui est en vert. ( Cf) est en rouge.
Oui, excuser moi, je me suis trompé Cg est croissant j'aurais du faire la flèche de l'autre coté.
Sinon le reste est bon ?
Pouvez vous m'aider pour le 2.
-
les valeurs centrales pour x sont fausses.
Pour la question 2,
tu appliques la règle des signes :- par + donne ....
-
Cchat dernière édition par
oups.. excuser moi je me suis trompé pour l'image, la voici :
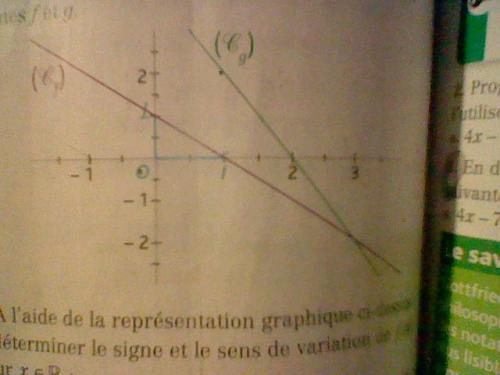
je l'ai modifié dans mon premier post, c'est celle ci la bonne image l'autre je m'étais trompé. Pouvez vous me dire si maintenant mes réponses sont bonnes s'il vous plait et m'aider pour le 2.. Merci d'avance.
-
C'est correct, suis les indications de mon précédent mail pour la résolution de la question 2.
-
Cchat dernière édition par
Un produit de 2 facteurs est >= 0, si ses 2 facteurs sont du même signe. Ici - par + donne - donc le produit de 2 facteurs n'est pas >= 0.
c'est ça ? je dois écrire comme ça ? il faut mieux rédiger non ? il faut faire quoi ensuite ?
-
Tu cherches les domaines pour lesquels les deux fonctions sont
positives,
négatives
ou
....
-
Cchat dernière édition par
Noemi
Tu cherches les domaines pour lesquels les deux fonctions sont
positives,
négatives
ou
....euuu ou égale à 0 ?????
-
ou positive et négative.
-
Cchat dernière édition par
Je cherche quels domaines ? Je comprend pas.
La fonction Cf est positive sur l'intervalle [-2;1] et est négative sur l'intervalle [1;4]
La fonction Cg est positive sur l'intervalle [0,5 ; 2] et [2;3,5]c'est ça ?
-
Les deux fonctions sont positives pour x appartenant à ] -∞ à 1], donc f(x) x g(x) est positif sur cet intervalle.
Analyse les autres intervalles.
-
Cchat dernière édition par
Les deux fonctions sont négatives pour x appartenant à [1 à + ∞], donc f(x) x g(x) est négatif sur cet intervalle.
Voila. C'est ça ? C'est fini ?
-
C'est faux, vérifie.
-
Cchat dernière édition par
vous pouvez m'écrire la phrase avec les trous s'il vous plait car là je sais plus je suis embrouillé.
-
Cchat dernière édition par
aaaa je crois que c'est :
Les deux fonctions sont négatives pour x appartenant à [2 à + ∞], donc f(x) x g(x) est négatif sur cet intervalle.c'est ça ?
Et là c'est fini ?
-
Oui
les deux fonctions sont négatives pour x appartenant à l'intervalle [2 ; +∞[, donc le produit f(x) x g(x) est positifsur cet intervalle.
Reste l'intervalle [1 ; 2]
....
-
Cchat dernière édition par
La fonction Cf est négative pour x appartenant à l'intervalle [1;2], et la fonction Cg est positive pour x appartenant à l'intervalle[1;2]; donc le produit f(x) x g(x) est négatif sur cet intervalle.
C'est bon ?
C'est fini ?
-
C'est juste.
-
Cchat dernière édition par
Donc là l'exercice est fini ?
-
Oui,
la question 2 est finie.
-
Cchat dernière édition par
D'accord. Merci.
-
Cchat dernière édition par
Mais peut être pour le tableau de signes j'aurais peut être du marquer :
Pour f(x)x : -l'infini au lieu de -2 .... 1 ....+ l'infini au lieu de 4
f(x) : .............................+.....-Non ?
et pour le tableau de variation aussi au lieu de mettre que c'est décroissant de -2 à 4 j'aurais du mettre que c'est décroissant de +l'infini à - l'infini non ?
-
Pour les deux droites tu peux mettre décroissant de -∞ à +∞ . Tu places au milieu, l'abscisse du point qui coupe l'axe des x.
-
Cchat dernière édition par
L'abscisse du point qui coupe l'axe des x c'est 0 non ????
-
Non,
pour f c'est x = 1 et pour g c'est x = 2
-
Cchat dernière édition par
Alors voici le tableau de signe et le tableau de variation pour le 1) a) :
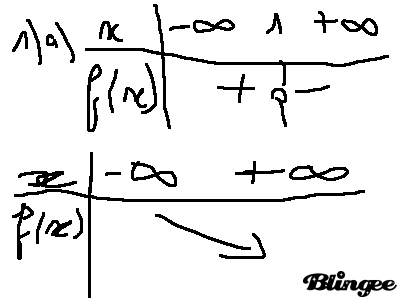
-
C'est juste.
-
Cchat dernière édition par
et voici le tableau de signe et de variation du 1)b) :
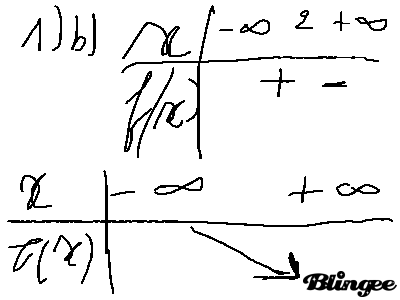
-
Cchat dernière édition par
Mais comme on demande <= 0, il faut aussi ajouter les valeur pour lesquelles chaque fonction = 0, puisque le produit est alors aussi = 0. non ?????
-
Oui, tu prends les valeurs qui annulent le produit.
Les solutions de l'équation f(x) g(x) ≥ 0 sont ....
-
Cchat dernière édition par
Les solutions de l'équation f(x) g(x) ≥ 0 sont .... je ne sais pas
-
Fais le bilan des résultats précédents.
-
Cchat dernière édition par
Les solutions de l'équation f(x) g(x) ≥ 0 sont ] -∞ à 1], [2 ; +∞[ et [1;2].
C'est bon ?
-
Cchat dernière édition par
Pouvez vous me dire si toutes mes réponses sont bonnes.
- a.
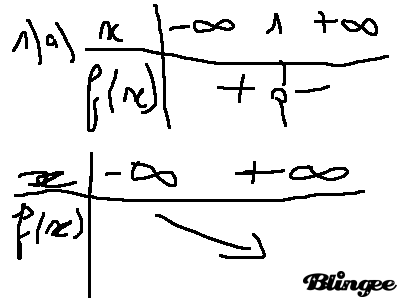
b.
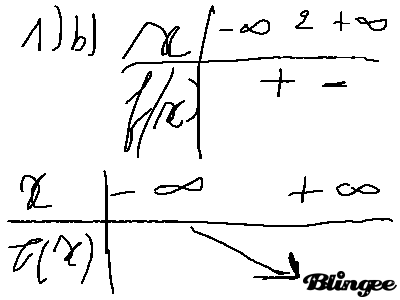
- Les deux fonctions sont positives pour x appartenant à ] -∞ à 1], donc f(x) x g(x) est positif sur cet intervalle.
les deux fonctions sont négatives pour x appartenant à l'intervalle [2 ; +∞[, donc le produit f(x) x g(x) est positif sur cet intervalle.
La fonction Cf est négative pour x appartenant à l'intervalle [1;2], et la fonction Cg est positive pour x appartenant à l'intervalle[1;2]; donc le produit f(x) x g(x) est négatif sur cet intervalle.
Donc Les solutions de l'équation f(x) g(x) ≥ 0 sont ] -∞ à 1], [2 ; +∞[ et [1;2].
-
Il manque le 0 dans le deuxième tableau.
Les solutions de l'équation f(x) g(x) ≥ 0 sont ] -∞ à 1]U [2 ; +∞[.
-
Cchat dernière édition par
Le deuxième tableau du 1) a) ou du 1)b) ou des deux ?
et j'ai oublié le 0 où ? entre quoi et quoi ?
-
Au 1 b) entre le + et le -.