Une aire, un périmètre sur un secteur
-
Mmaths-compliquer dernière édition par
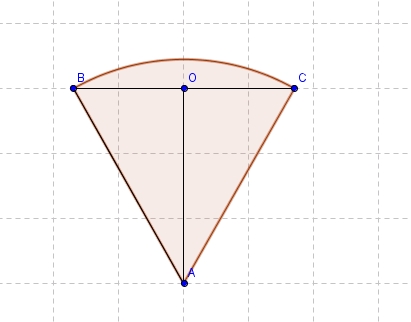
La forme d'un badge est le secteur ABC d'un cercle de centre A et de rayon AB. Le triangle ABC est équilatéral et à une hauteur perpendiculaire de 3 cm.
- trouver, la valeur exacte de la longueur AB
- Trouver avec π\piπ l'aire du badge
- Trouver avec π\piπ le périmètre du badge
Je n'arrive pas a trouvé les solutions ...

-
Bonsoir maths-compliquer,
Indique tes éléments de réponse et la question qui te pose problème.
En quelle classe es-tu ?
-
Mmaths-compliquer dernière édition par
Bonsoir, j'ai essaie de calculer la longueur de AB et je trouve AB = 3,00 mais je ne suis pas sur
Je bloque ensuite sur les questions 2 et 3 ...
-
Non, AB nest pas égal à 3.
Utilise la trigonométrie
a = h / sin60°
-
Mmaths-compliquer dernière édition par
Je ne vois pas pourquoi on utilise 60°
je pense que mon erreur viens de la car j'ai utiliser 90°
-
Mmaths-compliquer dernière édition par
-
Mmaths-compliquer dernière édition par
Pour AB je trouve 2√3 c'est bien ça ?
-
C'est le résultat.
Le triangle ABC est équilatéral, donc ses angles sont égaux à 60°.
-
Mmaths-compliquer dernière édition par
D'accord c'est bien ce que j'ai trouvais
Je me suis mis sur les autres questions et j'ai trouver pour l'aire 3π/2 et pour le périmètre 6+3π/3
= 6+π
Est-ce cela ?
-
Non,
Indique tes calculs.
-
Mmaths-compliquer dernière édition par
Pour l'aire :
π × r²× x/360
avec x en degré qui représente la valeur de l'angle BAC
donc j'obtiens: π×3²×60/360
=540π/360
Aire =3π/2Pour le périmètre:
=r×(2+π× X/180)
=3×(2+π×60/180)
=3×(2+ 60π/180)
=3×(2+π/3)
=6+3π/3
=6+π
-
Le rayon n'est pas égal à 3 mais à 2√3.
-
Mmaths-compliquer dernière édition par
Ah voilà mon erreur :$ je comprend mieux merci je vais rectifier tout cela