arithmétique: nombre premier

Bonjour , j'ai un DM que je ne comprends pas , votre aide sera la bienvenue :

Marcel Pagnol pensait avoir trouvé une formule magique qui permettait de trouver des nombres premiers :
<< Je crois avoir trouvé une formule qui permet de fabriquer des nombres premiers :
c'est la petite équation suivante .
x et x+2 sont deux nombres impairs consécutifs comme 55 et 7, ou 17 et 19, etc ;
x+(x+2) + x(x+2) est premier .>>
Utiliser une calculatrice ou un tableur pour donner les vingt premiers entiers naturels x qui infirment la proposition de Marcel Pagnol .
2.Vérifier que n²+n+41 est premier pour tout entier n tel que -40x40
3.Donner 3 valeurs de n pour lequelles n²+n+41 n'est pas premier .
4. En fait , les nombres A tels que n²+n+A est premier pour 0nA-1 sont dits nombres chanceux d'Euler .
trouver, en plus de 41, deux autres nombres chanceux d'Euler.
En fait on ne connaît pas de fonction qui génère tous les nombres premiers

voila merci d'avance

Bonjour eas,

Indique tes éléments de réponse et la question qui te pose problème.

La question 2 est-elle complète ?

x X+2 x+(x+2)+x(x+2) n²+n+41
3 5 8 1 43
5 7 12 2 47
11 13 24 3 53
17 19 36 4 61
29 31 60 5 71
41 43 84 6 83
59 61 120 7 97
71 73 144 8 113
101 103 204 9 131
107 109 216 10 151
137 139 276 11 173
149 151 300 12 197
179 181 360 13 223
191 193 384 14 251
197 199 396 15 281
227 229 456 16 313
239 241 480 17 347
269 271 540 18 383
281 283 564 19 421
311 313 624 20 461
347 349 696 21 503
419 421 840 22 547
23 593

Bon voila j'ai fais un tableau , c'est la question en effet qui me pose un problème je ne sais pas par où je pourrais commener

Pour la question 1, il faut donner les 20 premiers entiers naturels x qui infirment la proposition.

La question 2 est-elle complète ? A quoi correspond -40x40 ?

Ok j'ai compris
2)il y'a une erreur de frappe : c'est -40≤x≤40
Or quand je vérifie n²+n+41 , d'apres le tableur de ma calculatrice , je trouve bien en ennfet que n²+n+41 est premier pour tout entier naturel -40≤x<40 Oui j'ai bien mis < car pour x= 40 je trouve 1681 qui n'est pas premier , je ne sais pas si je suis dans le bon chemin

Ce doit être < 40.

j'ai envoyé un message à mon prof tout juste avant pour savoir si il ya une erreur , Mais est-ce que je peux répondre à cette question (2) de cette façon ?

La question 2 est juste une vérification, donc ta réponse est correcte.

Pour la question 3 , je ne trouve que pour n = 40 ,

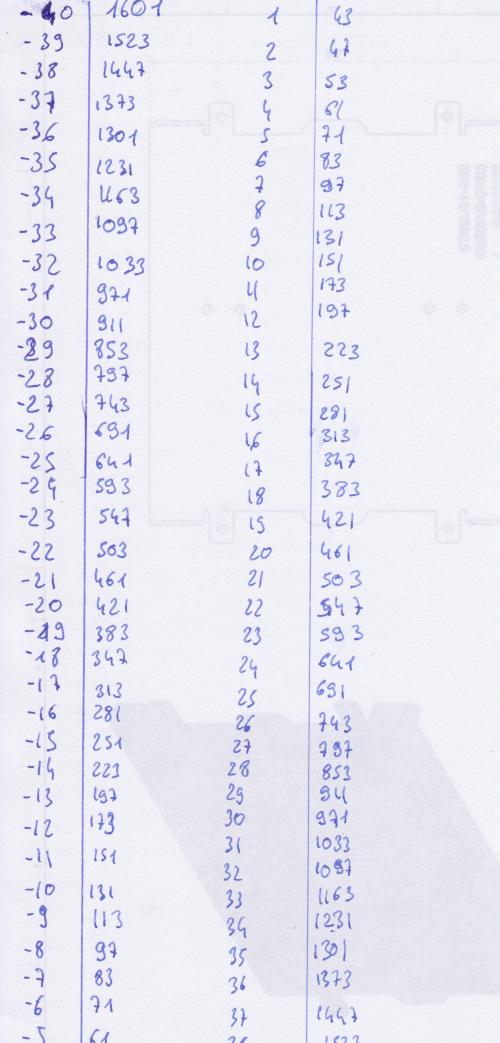
$fichier math$

Voila pour tableau que j'ai fait à main levée , mais je ne vois q'un seul valeurs de n pour lequelles n²+n+41 n'est pas premier qui est 40 Est-ce normal ?

Pour la 4
les nombres chanceux A sont ceux pour lesquels les entiers n²+n+A sont tous premiers, avec

cela impose déjà que A soit premier, car pour n=0, l'expression n²+n+A se résume à A, qui doit donc être premier

mais il est facile de voir que pour n=A-1, n²+n+A n'est jamais premier, puisque en remplaçant n par A-1, on trouve (A-1)²+(A-1)+A=A²

d'ailleurs, 1681=41²
Mais apres je n'arrive plus à trouver d'autre nombre chanceux

Pour la question 3, il faut chercher des valeurs supérieures à 41.

Je viens de découvrir qu'il n'y a pas de nombre chanceux supérieur à 41 . De plus , il n'est pas demander de trouver des nombres chanceux supérieur à 41 .

Je répondais à la question 3, trouver 3 valeurs de n pour lesquelles n²+n+41 (donc > 41) n'est pas premier.

Pour la question 4) Il existe 5 nombres chanceux d'Euler, le plus grand est 41.

Pour la question 3, d'apres mon tableur il ya 44,49,56 mais est-ce que je peyx répondre de cette facon par exemple : " D'après le tableur de ma calculatrice on a n=44 ou 49 ou 56 " ou bine il y'a des calcules à faire ?
Suite à mes recherches , j'ai trouvé comme nombre chanceux pour la question 4) 3,5,11,17 ,et je n'ai pas trouvé plus que 17 est-ce normal ? De plus , ces nombres chanceux j'ai les ai trouvé à la mimine , c'est-à-dire que j'ai chercher un par un , mais est-ce qu'on peut les trouver par calcule , et est-ce que je peux répondre à cette question sans faire des calcules , seulement en essayant et en vérifiant un par un des nombres premier ( à la mimine )

Il est indiqué dans l'énoncé avec une calculatrice ou un tableur,

Donc tu peux indiquer que tu as utilisé le tableur de ta calculatrice.