Déterminer l'expression d'une suite

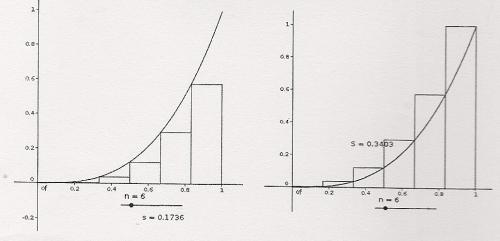
$fichier math$
on a représenté la fonction cube f(x) = x³ sur l'intervalle [0;1]. On se propose de calculer l'aire A du domaine limité par la courbe, l'axe des abscisses et la droite d'équation x=1 : on partage l'intervalle [0;1] en n intervalles de même longueur (n≥1) pour définir n rectangles intérieurs au domaine et n rectangles extérieurs.
On note Un la somme des aires des rectangles intérieurs et Vn la somme des aires des rectangles extérieurs. On obtient ainsi deux suites de réels (Un) et (Vn) qui encadrent l'aire A cherchée : Un≤A≤ Vn.

Calculer U1, V1, U2, V2, U3, V3.
Quelle est l'aire d'un rectangle intérieur (respectivement extérieur ) construit sur un intervalle du type [k/n ; k+1/n], avec 0≤k≤n-1 ?
En déduire que, pour tout réel, :
Un = 1/n^4 (0³+1³+...+(n-1)³) et Vn = 1/n^4 (1³+2³+...+(n-1)³+n³)
Merci d'avance !!

Bonsoir julie28,

Indique tes éléments de réponse et la question qui te pose problème.
U1 = ...
V1 = ...

Bonjour,
la question qui me pose problème est la question 2, je ne comprends ce qui faut faire ?

Comment as -tu calculé U1, U2 ?

Exprime Uk

Idem pour Vk

Oopss ! on m'a dit qu'il fallait calculer la surface d'un triangle pour avoir U1,... mais je ne vois pas pourquoi !!

Pas d'un triangle mais d'un rectangle.

oui c'est une erreur de ma part
cependant pour U1 je trouve 1 est-ce bon ?

et V1 = 1 ?

Encore une erreur de ma part U1 = 0 ?

Indique tes calculs.

j'ai utilisé ceux de la question 3 !!

Tu ne peux pas utiliser les relations de la question 3.

Cherche les dimensions du rectangle.

Le premier rectangle
Pour U, 0 et 1/n, soit U1 = 0
Pour V, 1/n³ et 1/n soit V1 = $1/n^4$
....

Merci beaucoup, j'ai eu le temps de faire les autres questions cependant je ne comprends pas du tout ce qu'il faut faire à la question 2 !