Déterminer l'ensemble de définition d'une fonction et tracer courbe

[loulou08]

Bonsoir à tous,

Pouvez-vous m'expliquer ce que je n'es pas compris merci

Partie A

Soit f : $x$ $⟹$ $-(x+1{)}^3+2x$

1. Déterminer l'ensemble de définition de f.

Réponse: On peut effectuer le calcul de f(x) pour toute valeur de x, donc $Df=\mathbb{R}$

2. Après avoir établi un tableau de valeurs bien choisi, tracer la courbe de f dans un repère orthonormé.

Réponse

TABLEAU:

GRAPHIQUE:

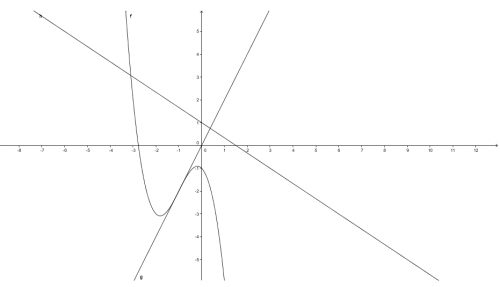
3. Graphiquement établir le tableau de variations de f sur son ensemble de définition.

Réponse

TABLEAU DE VARIATION:
$\begin{array}{|c|ccccccc||}x&-\infty&&-2&&0&&+\infty \{signe}& &-&3&-&1&& \{variation}&&\searrow&&\nearrow&&\searrow&&\end{array}$

4. Graphiquement établir le tableau de signes de f sur son ensemble de définition.

Là je ne vois pas comment il faut faire.

Partie B

Soit g :$x$ $⟹$ $2x$ et h : $x$$⟹$ $-\frac{2}{3}x+1$

1. Déterminer les ensembles de définition de g et de h.

Là je ne vois pas comment il faut faire.

2. Après avoir rappelé la nature de g et de h, tracer leurs représentations graphiques dans le même repère que celle de f.

***Réponse :****La nature de g c'est que sais une fonction linéaire et la nature de h c'est que sais une fonction affine. Pour leurs représentations graphiques ( Voir graphique de la Partie A ).
*
3) Établir algébriquement les tableaux de signes de g et de h sur leurs ensembles de définition.

Là je ne vois pas comment il faut faire.

4. Résoudre algébriquement l'équation $f(x)=g(x)$

*Là je ne vois pas comment il faut faire.*Partie C

Soit k :$x$ $⟹$ $\frac{2x-1}{-3x+2}$ et L : $x$ $⟹$ $\sqrt{-4x-1}$

1. Déterminer l'ensemble de définition de k.Réponse:$\frac{2x-1}{-3x+2}$

$-3x+2=0$
$-3x=-2$
$x=\frac{2}{3}$

$Dk=\mathbb{R}-${$\frac{2}{3}$}

2. Déterminer l'ensemble de définition de L.Réponse:

[Noemi]

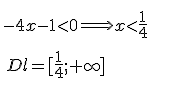
Bonsoir loulou08

Pour les tableaux de signes, tu cherches pour quelles valeurs de x la fonction est positive, puis négative.

Pour l'ensemble de définition de g et h, tu appliques le même raisonnement que pour f.

Pour la résolution de f(x) = g(x), tu résous 2x = -2x/3 + 1

Le domaine de définition de L est fauxRésous -4x-1 ≥ 0

[loulou08]

Ok merci Noemi je regarde ça après manger.

[loulou08]

Partie B

1. On peut effectuer le calcul de g(x) pour toute valeur de x, donc $Dg=\mathbb{R}$.

On peut effectuer le calcul de h(x) pour toute valeur de x, donc $Dh=\mathbb{R}$

4. Résoudre f(x)=g(x)

$2x=-\frac{2x}{3}+1$
$2x+\frac{2x}{3}-1$
$\frac{6x}{3}+\frac{2x}{3}-\frac{3}{3}=0$
$\frac{8x-3}{3}=0$
$8x-3=0$
$8x=3$
$x=\frac{3}{8}$

La solution de l'équation f(x)=g(x) est $\frac{3}{8}$

3. Pour le tableau des signes je vois comment il faut faire, mais avec le graphique sa me pose problème et pareil pour leurs ensemble de définition :frowning2: , si vous pouvez m'apporter un peut plus d'explication je suis preneur

[Noemi]

Pour le tableau de signes, tu analyses la courbe :
Par exemple pour g(x) = 2x (fonction linéaire),
La courbe est en dessous de l'axe des abscisses pour x< 0,
et est au dessus de l'axe pour x >0
donc f(x) < 0 si x < 0 et f(x) >0 si x > 0

Tu cherches en premier les valeurs de x telles que la courbe coupe l'axe des abscisses.

[loulou08]

Tableau:

X
...?
...?
g(x)

En fait c'est ou qui y a les pointillés que je sais pas quoi mettre

[Noemi]

Pour quelle valeur de x, f(x) = 0 ?

[loulou08]

Faut déterminer l'antécédent non ?

[Noemi]

Oui,

Utilise le graphique.

[loulou08]

La valeur de x est donc d'environ -2.9

[Noemi]

Ce n'est pas -2,77 ?

[loulou08]

oui j'ai tapé la fonction sur la calculatrice et c'est bien 2,77.

Ensuite on fait comment ?

[Noemi]

Si x compris entre -∞ et -2,77, f(x) > 0
si x > -2,77, f(x) .....

[loulou08]

Si x > -2,77, f(x) < 0 ?

[Noemi]

oui,

c'est correct.

[loulou08]

Bonjour Noemi,

Donc grâce à ça je devrais arriver à faire le tableau ?

[loulou08]

Partie C

2. $-4x-1$ ≥ $0$$⟹$$x$≤ $-\frac{1}{4}$

$D_l=$$[-\frac{1}{4};+\infty ]$

[Noemi]

Non

x ≤ -1/4 donne pour ensemble ]-∞ ; -1/4]

[loulou08]

ok merci Noemi et pour le tableau de signe on si prend comment ?

[Noemi]

Tableau de signes pour f
x -∞ -2,77 +∞
f(x) + 0 -

[loulou08]

Tableau pour f

Et pour le tableau de signe de g et e h, il faut résoudre une équation ?

2x = 0
... ?

[Noemi]

Il manque la valeur -2,77 pour f.

Pour g et h, tu peux résoudre l'équation g(x) = 0 et h(x) = 0.

[loulou08]

Oups oui un petit oublie je corrigerais ça merci Noemi.

donc pour g(x)=0

2x=0
x=0

et pour h(x)=0

$-\frac{2}{3}x+1=0$
$-\frac{2}{3}x+\frac{3}{3}=0$
$-2x+3=0$
$-2x=-3$
$x=\frac{3}{2}$

Ça semble correct ?

[Noemi]

C'est correct.

[loulou08]

tableau de signe de g

X -∞ 0 +∞
f(x) ?? ??

Comment on peut savoir si c'est positif ou négatif ?
Grâce au graphique ?

[Noemi]

Soit tu résous une inéquation, soit tu analyses le graphe.
2x>0 si x ......
Le graphe est au dessus de l'axe des abscisses si x .....

[loulou08]

Je pense qu'il faut résoudre une inéquation vue que l'énoncé dit établir algébriquement.

donc pour g : 2x>0 si x>0
et pour h : -2/3x+1>0 si x < 3/2

Ça serait juste ?

[Noemi]

C'est juste.

[loulou08]

Tableau de signe pour g:

X -∞ 0 +∞
g(x) - 0 +

??

Tableau de signe de h:

X -∞ 3/2 + ∞
h(x) + 0 -

??

[Noemi]

C'est juste.

[loulou08]

Merci beaucoup pour ton aide Noemi, tout le reste semble juste ?

[Noemi]

oui cela semble correct.

[loulou08]

Merci beaucoup et bonne après-midi à toi