Conjecturer la position de deux droites et démontrer
-
AAmandine2b dernière édition par Hind
Bonjour et bonne fin d'année à tous.
Voici mon exercice :
Soit O un point du plan de deux demi-droites (d1) et (d2) d'origine O perpendiculaires en O.
a) Faire une figure avec un logiciel de géométrie dynamique (par exemple GEOGEBRA)
et créer un point mobile M de la droite (d1) et un point mobile de la droite (d2), avec M et N distincts du point O.b) Tracer la bissectrice (DELTA) de l'angle MON, puis construire, toujours avec ce logiciel, les symétriques M'et N'
des points M et N par rapport à cette droite (delta)c) Construire le point I milieu du segment [M'N'], puis imprimer la figure ainsi réalisé que vous rendrez avec votre copie.
d) En jouant avec la position des points M et N, que peut-on conjecturer sur les droites (OI) et (MN)?
e) Démontrer sur votre copie le conjecture de la première partie, par une méthode de votre choix.
Voici ma figure :
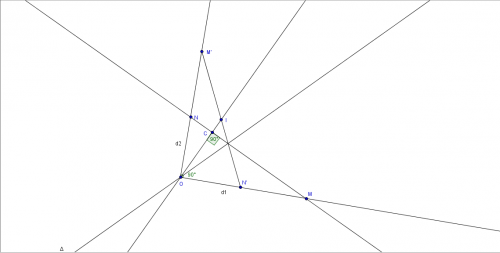
Je n'arrive pas à démontrer que mes droites (OI) et (MN) sont perpendiculaires,
Merci par avance pour votre aide
-
Bonjour Amandine2b,
Une piste,
Utilise un repère et les coordonnées des points pour montrer que les vecteurs OI et MN sont orthogonaux.
-
AAmandine2b dernière édition par
Deja je peux écrire que
om′⃗=2on⃗=on⃗+nm′⃗ om⃗=2on′⃗=on′⃗+n′m⃗ etom⃗.om′⃗=0\vec{om'} = 2\vec{on} = \vec{on} + \vec{nm'} \ \vec{om} = 2\vec{on'} = \vec{on'} + \vec{n'm} \ et \vec{om}.\vec{om'} = 0om′=2on=on+nm′ om=2on′=on′+n′m etom.om′=0
...
-
Pourquoi ce coefficient 2 ?
-
AAmandine2b dernière édition par
parce que on⃗+on⃗=om′⃗\vec{on} + \vec{on} = \vec{om'}on+on=om′
-
Les points N et M sont mobiles.
-
AAmandine2b dernière édition par
Oui excusez moi, je me suis trompée ...
ensuite je peux ecrire que oi⃗=on′⃗+n′i⃗\vec{oi} = \vec{on'} + \vec{n'i}oi=on′+n′iMais je ne sais pas comment continuer ensuite ...
-
Utilise les coordonnées des vecteurs.
-
AAmandine2b dernière édition par
Je ne peux pas arriver à demontrer d'une autre façon ? avec les égalités sur les angles par exemple ...?
-
Indique tes calculs avec les angles;
-
AAmandine2b dernière édition par
Je n'ai pas fait de calculs; mais je pensais utiliser le fait que ION' et M'OI sont deux triangles isocèles, donc les angles à la base sont égaux. Si je pouvais trouver la mesure de l'angle IOM' alors mon travail serait quasiment fini ...
-
N'oublie pas que les point M et N sont mobiles, donc les mesures des angles changent.
-
AAmandine2b dernière édition par
Cela ne change pas le fait que j'ai 2 triangles isocèles me semble-t-il, puisque I est le milieu de [M'N'] et donc (OI) est la médiane de OM'N' issue de O
-
C'est exact, les triangles seront toujours isocèles.
-
AAmandine2b dernière édition par
Je n'ai pas besoin de trouver une mesure exacte pour l'angle IOM' , puisque les points sont mobiles ... il faut que je trouve une égalité
-
Tu dois en déduire que l'angle OCM = 90°.
-
AAmandine2b dernière édition par
est ce que cela m'amène quelque part si je trouve que C est le centre de gravité du triangle ?