démonstration géométrique avec des coordonnées

Bonjour j'ai un DM sur géométrie et j'ai besoin d'aide dans la partie 2 de l’exercice 1
1.Construction et conjecture
a. avec le logiciel Geogebra, tracer un carré ABCD de coté AB variable, puis les triangles équilatéraux CDI et BCL, respectivement intérieur et extérieur au carré ABCD.Tracer la droite (AI).
b. En faisant varier le coté AB conjecturer une propriété sur les points A,I et L.

2 Preuve de la conjecture
a. Donner les coordonnées des point D,C,A et B dans le repère orthonormé (D;C;A)
b.Calculer les valeurs valeurs exactes des coordonnées des points I et L.
( on rappelle que cos60ª=1/2, sin60ª=√3/2 et tan60ª=√3
c. Démontrer finalement la conjecture émise dans la partie 1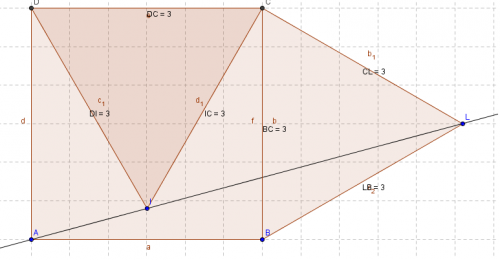

$fichier math$

edit : merci de donner des titres significatifs

Bonsoir duquemotta,

Indique tes résultats :
Coordonnées des points D, C, A, B.

c'est sa ce que je ne comprend pas.
je sais que si on deplace B les points A I et L sont toujours aligné.

merci

Dans le repère D C A,
D(0;0) ; C(1;0) ; A(0;1)
B(....)

B(0;1) vraiment je ne sais pas :S

B(0;1) vraiment je ne sais pas :S

Non
B(1;1)

calcule les coordonnées de L et I.

merci, pour les coordones de I je trace la hauteur issue de I dans le triangle DCi mais je ne sais pas comment continuer.

IH = UI sin60°
UH = UI cos 60°

Bonne nuit.

DCI est un triangle équilatéral.
Dans le repère orthonormé (D;C;A) on a : DC=1 et DI=1

Soit H le pied de la hauteur du triangle DCI issue de I
et K le pied de la hauteur du triangle DIA issue de I

cos IDC=DH/DI=DH car DI=1
donc : DH=cos60°=1/2 (Tous les angles d'un triangle équilatéral sont égaux et mesurent 60°))

De même sinIDC=HI/DI=HI car DI=1
donc HI=sin60°=√3/2
Or HI=DK donc DK=√3/2

Ainsi I (1/2 ; √3/2)

Le triangle (LBC) est équilatéral, et LB=LC=CB=1
Soit H' la projection orthogonale de L sur la droite (DC)
et K' la projection orthogonale de L sur la droite (BC)

L'angle LCH' mesure 30° (90°-60°)

cos LCH'=CH'/CL=CH' car CL=1

donc CH'=cos LCH'=cos 30°=sin 60°=√3/2 (angles complémentaires)

DH' = DC+CH' = 1+√3/2 = (2+√3)/2

sin LCH' = H'L/CL = H'L car CL=1

donc LH' = sin 30° = cos 60° = 1/2

Ainsi L ((2+√3)/2 ; 1/2)

Soit (d) la droite passant par les points A (0 ; 1) et I (1/2 ; √3/2)

(d) a pour équation y = ax + b

Calculons a et b en exprimant le fait que A ∈ (d) et I ∈ (d)

On trouve d'une part : 1 = a.0 + b et d'autre part : √3/2 = a/2 + 1

Finalement : b = 1 et a = √3 - 2 et (d) : y = (√3 - 2)x + 1

Il suffit de vérifier que l'on a bien L ((2+√3)/2 ; 1/2) ∈ (d)

Les points A, I et L sont bien alignés.

Le but de cet exercice est de montrer que quelque soit la longueur du côté du carré ABCD, quand on se place dans le repère orthonormé (D;C;A), cette longueur n'a plus de sens puisqu'elle vaut toujours 1 dans ce repère.
Et l'on peut démontrer que les points A, I et L sont toujours alignés.