Signe de ma dérivée

Bonjour,

J’éprouve quelques difficultés à trouver le signe de ma dérivé =/
Je l'ai écrite sur word et fait une copie d'écran de ma fonction et des mes calculs pour la dérivée(je trouve cela plus clair^^).

$fichier math$

En pensant que nous sommes sur l'intervalle ]0;5[.
On peut déjà admettre que, sur cet intervalle, le dénominateur est positif, donc le signe dépend du numérateur. Hélas je ne sais pas par où commencer après ça...

Pourriez-vous me lancer sur une piste ?
Si ma dérivé est fausse, pourriez-vous m'aider à la corriger ?
Merci d'avance.

Bonjour Pandafurtif,

Développe le numérateur et cherche son signe.

Merci de ce conseil, le cube me faisait un peu peur mais ça a été, j'ai trouvé :

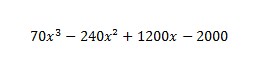
$fichier math$

Dois-je le dériver pour tomber sur du second degré, trouver le signe de cette dérivé puis les variations et me servir de ces variations pour trouver le signe de la fraction ?

Oui, c'est la méthode.

D'accord, merci
Je fais mes calculs et je posterai ça plus tard dans la journée.

Voilà où j'en suis arrivé avant d'être bloqué

$fichier math$

Une erreur dans la dérivée, c'est 210x²,

Cherche la valeur qui annule f'(x)

Ah effectivement >< Je corrige ça, merci

La valeur qui annule 210x²-480x+1200 ? Il n'y en existe pas puisque Δ est négatif ?

Non,

la valeur qui annule h, x = 2.

Ah d'accord, mais je ne vois pas comment trouver ce 2 =/

Tu cherches avec la calculatrice, l'image pour x = 1, 2 et 3.

Ah ? Il n'y a pas de calcul à faire ?
Ok, merci beaucoup alors =D

Juste f(1), f(2) et f(3).

J'en ai parlé a des personnes de ma classe, le professeur a donné une solution que j'ai essayé de refaire

$fichier math$

Malheureusement il semble que j’ai une erreur de signe, je ne la trouve pas =/

Bien

compare
(3x)³ avec [2(5-x)]³
soit
3x avec 10-2x
3x > 10-2x si
.....

Mais j'ai trouvé $2(5-x)]^3$ soit (-10+2x) et non le contraire. Que dois-je changer plus haut pour en arriver là ?

Tu étudies le signe de -16(5-x)³ +54x³ ce qui revient à comparer
16(5-x)³ avec 54x³
car
-16(5-x)³ +54x³ > 0 équivalent à
54x³ > 16(5-x)³

Ah d'accord, il faut donc "transformer" les termes après avoir mis sous forme d'inéquation.
Merci beaucoup pour toute cette aide, ça devrait être bon maintenant, merci encore