Dresser le tableau de variation d'une fonction rationnelle et résoudre inéquation
-
Ddavid06 dernière édition par Hind
Bonsoir,
Soit fff la fonction définie par f(x)=−53x+2−x−4f(x) = -5 \frac{3x+2}{-x-4}f(x)=−5−x−43x+2 .
- Déterminer l'ensemble de définition de f.
Réponse:f(x)=−53x+2−x−4f(x) = -5 \frac{3x+2}{-x-4}f(x)=−5−x−43x+2
-x-4 = 0
-x = 4
x=-4Df=R−D_f = \mathbb{R}-Df=R− {−4-4−4}
- Établir le tableau de variation de f sur son ensemble de définition.
Réponse : f(1)=−531+2−1−4=5f(1) = -5 \frac{31+2}{-1-4} = 5f(1)=−5−1−431+2=5
$\begin{array}{|c|ccccccc||}x&-\infty&&1&&+\infty \{signe}& &&5&\{variation}&&\nearrow&&\searrow&&\end{array}$
- En déduire l'ensemble des solutions de l'inéquation f(x)≥0.
Je n'ai aucune idée pour résoudre cette inéquaton.
-
Bonsoir david06,
La réponse pour la question 1 est correcte.
Le tableau de variation est faux.
Pour la question 3 il faut analyser les variations de f.
-
Ddavid06 dernière édition par
Bonsoir Noemi,
Peux-tu m'apporter plus d'explication pour la tableau de variation parce que je ne vois pas comment il faut faire.
-
Connais tu le tableau de variation de fonction qui a x associe (ax+b)/(cx+d) ?
-
Ddavid06 dernière édition par
Non je n'ai pas vue ça en cours Noemi
-
Comment procèdes tu pour établir un tableau de variation ?
-
Ddavid06 dernière édition par
Le plus souvent le tableau de variation je le faisait a l'aide d'une courbe, mais pour là on peut pas.
-
Quel type de courbe (fonction) connais tu ?
-
Ddavid06 dernière édition par
Par exemple cette fonction f(x)=(2/3x+1)(-3x+3)
-
Comment construis tu le tableau de variation de cette fonction ?
-
Ddavid06 dernière édition par
Grâce à la courbe, quand la courbe monte ( croissante) et quand la courbe descend (décroissante).
Mais pour cette fonction f(x)=−53x+2−x−4f(x) = -5 \frac{3x+2}{-x-4}f(x)=−5−x−43x+2 il faudrait établir un tableau de signe et ensuite grâce à ça on peut faire le tableau de variation ?
-
Pas très rigoureux comme méthode.
Représente la fonction sur la calculatrice.
-
Ddavid06 dernière édition par
Ça me fait cette courbe:
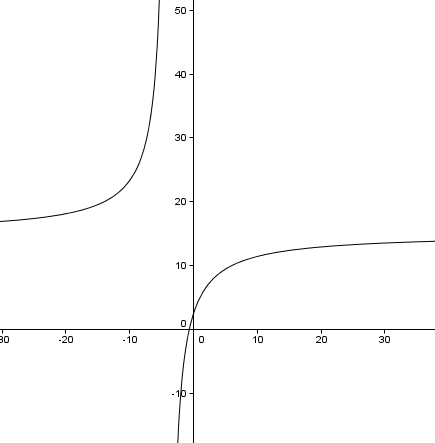
-
Oui,
Donc fonction croissante sur les intervalles de l'ensemble de définition.
-
Ddavid06 dernière édition par
Bonjour Noemi
Donc je pars de -4 à +∞ ?
-
Pour x :
x -∞ -4 +∞
-
Ddavid06 dernière édition par
$\begin{array}{|c|ccccccc||}x&-\infty&&-4&&+\infty \{variation} \{de}\{H}&&\nearrow&&0&&\nearrow&&\end{array}$

-
en -4 la fonction n'est pas définie donc // (et non 0)
-
Ddavid06 dernière édition par
Merci donc ça donne :
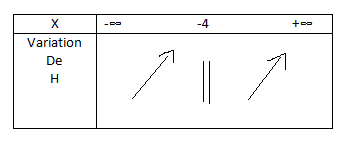
-
C'est correct.
-
Ddavid06 dernière édition par
Merci beaucoup Noemi,
Citation
- En déduire l'ensemble des solutions de l'inéquation f(x)≥0.
L'ensemble des solutions de l'inéquation f(x)≥0 est -4.

-
Ddavid06 dernière édition par
Et 0

-
Ddavid06 dernière édition par
Je résume :
3x+2 = 0
3x= -2
x=-2/3-x-4=0
-x=4
x=-4L'ensemble des solutions de l'inéquation f(x)≥0 est -2/3 et -4
-
Tu cherches les valeurs de x pour lesquelles, le graphe de f est au dessus de l'axe des abscisses.