Fonction recette, coût et bénéfice

Bonjour à tous,

J'aimerais avoir de l'aide pour cet exercice, merci beaucoup à vous

Une entreprise agroalimentaire produit mensuellement entre 0 et 100 tonnes de biscuits. On pose x le nombre de tonnes de biscuits produits.
Pour $x$ ∈[0;100], on pose $R (x)$ la recette et $C (x)$ le coût en fonction du nombre de tonnes de biscuits produits, exprimés en milliers d'euros.
Le comptable de l'entreprise estime que $R(x)=2x+30+2250070−x2R(x)=2x+30+\frac{22500}{70-\frac{x}{2}}$ et $C (x) = 6 x + 330$ .

a) Exprimer en fonction de $x$ la fonction bénéfice B défini sur [0;100].

Réponse : $B (x) = R (x) - C (x)$
= $2x+30+2250070−x2−(6x+330)2x+30+\frac{22500}{70-\frac{x}{2}} - (6x+330)$

Est-ce qu'il faut commencer comme ça pour exprimer en fonction de x la fonction bénéfice B défini sur [0;100]

b) Montrer que pour tout $x$ ∈[0;100], $B(x)=2x2−130x+150070−x2B(x)=\frac{2x^2-130x+1500}{70-\frac{x}{2}}$

Réponse : $2x+30+2250070−x2−6x−3302x+30+\frac{22500}{70-\frac{x}{2}} -6x-330$
$=−4x−300+2250070−x2=-4x-300+\frac{22500}{70-\frac{x}{2}}$
$=(−4x−300)(70−x2)70−x2+2250070−x2=\frac{(-4x-300)(70-\frac{x}{2})}{70-\frac{x}{2}}+\frac{22500}{70-\frac{x}{2}}$
$=−280x+2x2−21000+150x+2250070−x2=\frac{-280x+2x^2-21000+150x+22500}{70-\frac{x}{2}}$
$=2x2−130x+150070−x2=\frac{2x^2-130x+1500}{70-\frac{x}{2}}$

Est-ce juste

c) En déduire que pour tout $x$ ∈[0;100], $B(x)=4(x−50)(x−15)140−xB(x)=\frac{4(x-50)(x-15)}{140-x}$

Si $4(x−50)(x−15)140−x=2x2−130x+150070−x2\frac{4(x-50)(x-15)}{140-x}=\frac{2x^2-130x+1500}{70-\frac{x}{2}}$ *** alors*** $2x2−130x+150070−x2=4(x−50)(x−15)140−x\frac{2x^2-130x+1500}{70-\frac{x}{2}}=\frac{4(x-50)(x-15)}{140-x}$
$=4(x2−15x−50x+750)140−x=\frac{4(x^2-15x-50x+750)}{140-x}$
$=(4x2−60x−200x+3000)/21402−x2=\frac{(4x^2-60x-200x+3000)/2}{\frac{140}{2}-\frac{x}{2}}$
$=2x2−130x+150070−x2=\frac{2x^2-130x+1500}{70-\frac{x}{2}}$

Est-ce juste

2.a) Établir le tableau de signe de la fonction B sur [0;100].

Résoudre x-50=0
x=50

Résoudre x-15=0
x=15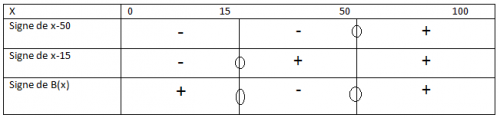

$fichier math$

b) Résoudre sur [0;100] l’inéquation $B (x)$ <0.

Réponse : L'inéquation B(x)<0 a pour ensemble de solution ]15;50[.

Est-ce juste

c) En déduire pour quelle(s) production(s) l'entreprise fait des bénéfices.

Réponse : D'après le tableau de signe l'entreprise fait des bénéfices de 0 à 15 tonnes de productions de biscuits et de 50 à 100 tonnes de productions de biscuits.

Est-ce juste

Dans un repère orthogonal adapté, représenter graphiquement la fonction B sur [0;100].

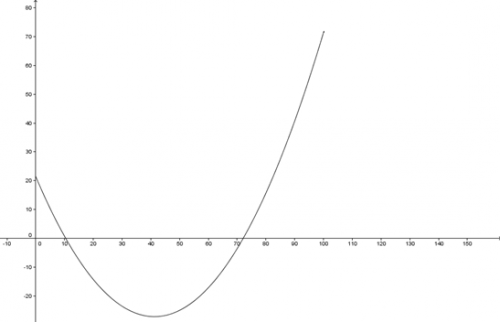
$fichier math$

Graphiquement, déterminer pour quelle(s) production(s) le bénéfice est supérieur à 100 000 euros.

Réponse : On ne peut pas la déterminer car c'est compris dans l'intervalle [0;100].

Est-ce juste

En 2008 la production mensuelle s'est maintenue à 70 tonnes. Calculer le bénéfice mensuel, pis le bénéfice annuel pour l'année 2008.

Réponse : $B(70)=4(70−50)(70−15)140−70≈62,857B(70)=\frac{4(70-50)(70-15)}{140-70}\approx 62,857$

Le bénéfice mensuel en 2008 est de 62,857 milliers d'euros.

$4(70−50)(70−15)140−70×12≈754,286\frac{4(70-50)(70-15)}{140-70}\times 12\approx 754,286$

Le bénéfice annuel en 2008 est de 754,286 milliers d'euros.

Est-ce juste

Les prévisions pour 2009 parlent d'une baisse de la production de 15% sur l'ensemble de l'année.

a) Calculer la production mensuelle prévue pour 2009.

Réponse : En 2008 la production mensuelle s'est maintenue à 70 tonnes et les prévisions pour 2009 parlent d'une baisse de la production de 15% sur l'ensemble de l'année.
Production mensuelle pour 2009

$70×0,7=4970\times 0,7=49$

La production mensuelle prévue pour 2009 est 49 tonnes.

Est-ce juste

b) Calculer le bénéfice prévisible pour l'année 2009.

Réponse : $\frac{4(49-50)(49-15)}{140-49}*12$ ≈ -17.934

Le bénéfice est négatif, soit un déficit de 17,934 milliers d'euros donc 17 934 €

Le bénéfice prévisible pour l'année 2009 est de 17 934 €.

Est-ce juste

Pouvez-vous m'aider SVP

Merci beaucoup

Personne pour m'aider :frowning2:

Bonjour,

Vérifie la programmation de la fonction pour le graphique et les questions suivantes.

Bonjour Noemi,

Faut changer l'axe des abscisses et des ordonnées et il faut s'exprimer en millier d'euros ?