géométrie, fonction
-
Ddavid06 dernière édition par
Bonjour,
Un point mobile M décrit le segment [AB] en partant de A et en se dirigeant vers B. Soit O un point en dehors de (AB) et H le projeté orthogonal de O sur [AB]. La distance AM est notée x, la distance OM est notée f(x). On donne AB=5cm, OH=HB=2cm.
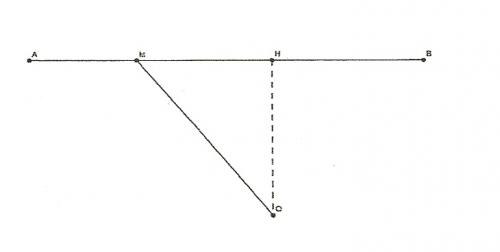
- a. Déterminer quelles valeurs peut prendre x.
x peut prendre toute les valeurs de A à B.
b. Vérifier que si M∈[AH], on a f(x) = (x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4.
MHO est un triangle rectangle en H. Donc, d'après le théorème de Pythagore, on a:
MO²=MH²+HO²
MO²=(x-3)²+2²
MO²=(x-3)²+4
MO²=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4Donc c'est vérifier que si M∈[AH], on a f(x)=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
c. Donner l'expression de f(x) lorsque M∈[HB].
Ici je pense qu'il faut utiliser le théorème de Pythagore mais je suis pas sur.
Merci pour votre réponse.
-
IIron dernière édition par
bonjour David06,
"x peut prendre toute les valeurs de A à B"
oui mais on attend de toi un encadrement de x ...
Puisque AB = 5 cm, x ∈ [ 0 ; 5 ]b.
MO
²=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4le carré à enlever (je suppose que c'est une erreur de frappe).
Tu es sûr que l'énoncé donne f(x) = (x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
MH = 3-x, ce ne serait pas pas f(x) = (3−x)2+4\sqrt{(3-x)^2+4}(3−x)2+4 ?
c. Donner l'expression de f(x) lorsque M∈[HB].
Ici je pense qu'il faut utiliser le théorème de Pythagore mais je suis pas sur.
Oui, même méthode, sauf que cette fois HM = x-3 (car x≥3 cette fois)
MO=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
-
Ddavid06 dernière édition par
bonjour Iron et merci pour ta réponse,
a.AB = 5 et OH=HB=2cm
donc quand M∈[AB], on a 0 ≤ x ≤ 5 ;x peut prendre les valeurs comprises dans l’intervalle [0 ; 5]
b. oui c'est une erreur de frappe sur mon brouillon je l'ai pas mis

Sur mon énoncé c'est bien f(x)=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
c. MO²=HM²+HO²
((x−3)2+4)2(\sqrt{(x-3)^2+4})^2((x−3)2+4)2=(x-3)²+2²
(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4=MO
-
IIron dernière édition par
a) OK
b) Si ton énoncé précise bien f(x)=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4 alors fais une petite pirouette :
AH = AM + MH
MH = AH - AM
MH = 3 - xalors
MO² = MH²+HO²
MO² = (3-x)²+2²
MO² = (3-x)²+4
MO² = [-1(x-3)]²+4
MO² = [x-3]²+4
soit
MO=(x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4c.
MO² = HM²+HO²
MO² = (x-3)²+2²
MO² = (x-3)²+4
soitMO = (x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
donc dans les deux cas, M∈[AH] ou M∈[HB], f(x) = (x−3)2+4\sqrt{(x-3)^2+4}(x−3)2+4
-
Ddavid06 dernière édition par
Merci beaucoup Iron
Bonne soirée

-
IIron dernière édition par
Je t'en prie, bonne soirée également.
-
Ddavid06 dernière édition par
Merci
-
Ddavid06 dernière édition par
Bonjour à tous,
j'aurais une autre question:
- On cherche le ou les points du segment [AB] situé(s) à la distance 3 du point O.
a.En utilisant les expressions de f(x), déterminer précisément la position de ce(s) point(s).
Je pense qui faut faire (x−3)2+4=3\sqrt{(x-3)^2+4} = 3(x−3)2+4=3, mais je n'arrive pas à la résoudre.
Merci pour votre aide
- On cherche le ou les points du segment [AB] situé(s) à la distance 3 du point O.
-
Ddavid06 dernière édition par
Quelqu'un pour m'aider ?
-
Bonsoir,
Elève l'expression au carré pour enlever la racine carré.
-
Ddavid06 dernière édition par
Bonjour,
Merci