Activité : pourquoi racine de -1?

Bonjour,

j'aurai besoin de votre aide pour un exercice de maths, ou plutôt une activité , avec laquelle je rencontre des difficultés.
Il s'agit d'une activité nommée Pourquoi √-1?

L'énoncé est le suivant

Cette activité a pour objectif d'introduire les nombres complexes : pourquoi les mathématiciens ont-ils eu besoin d'introduire la racine d'un nombre négatif, chose que nous avons prescrit jusqu'à présent ?

I. Un peu d'histoire
En 1545, Jérôme Cardan (Italien, 1501 − 1576) a proposé, dans son ouvrage Ars Magna, une méthode permettant de résoudre les équations polynomiales de degré 3.
Cette méthode permet de déterminer explicitement une des racines du polynôme de degré trois, un peu comme ce que l'on connait pour les trinômes du second degré.
Cette méthode 1 fonctionnait plutôt bien, jusqu'au jour où ...

II. Méthode de Cardan
Soit le théorème suivant, que l'on admet :

Une équation simple
Soit (E) l'équation x3 − 2x + 5 = 0.

Dresser le tableau de variations de la fonction f : x 􏰀→ x3 − 2x + 5.

pour cette question j'ai calculer la dérivée et j'ai trouvé 3x2 -2
et j'en ai déduis que f' était positive de - l'infini à -√2/3
négative de -√2/3 à √2/3
positive de √2/3 à + infini

En déduire qu'il existe un unique réel α tel que f(α) = 0.

pour cette question je bloque, j'ai tenté de calculer f(-√2/3) et f(2√3) mais je trouve des résultats qui me semblent incorrects étant donnés qu'ils n'intègrent pas 0. je trouve pour le premier 4,16 et le deuxième 5,8 ....

Appliquer la méthode de Cardan pour en déduire une valeur approchée à 10−3 près de α.
(méthode voir photo)

alpha : ^3√(-5/2 -1/2√643/27 )+ ^3√(-5/2 -1/2√643/27)
alpha environ = à 2,094

Une autre
Soit (E′) l'équation x3 − 15x − 4 = 0.

Dresser le tableau de variations de la fonction f : x 􏰀→ x3 − 15x − 4.

ici je trouve f' positif, négatif , positif

En déduire qu'il existe trois réels α,β,γ tel que f(α) = f(β) = f(γ) = 0. 3. Peut-on appliquer la méthode de Cardan sur cette équation ?

ici je n'ai aucune idée de comment m'y prendre...

peut-on appliquer la méthode de Cardan sur cette équation.

Non car en l'appliquant on trouve ∆= -13068 strictement négatif
et même en appliquant la formule on obtiendrait des racines carrées de nombres négatifs.

III. La méthode Bombelli
Raphaël Bombelli (1526 − 1572) propose alors de supposer que l'on peut prendre la racine d'un nombre négatif.

Racine d'un nombre négatif
Exprimer ce que donne la méthode de Cardan dans le cas de l'équation x3 − 15x − 4 = 0, en supposant que l'on puisse prendre la racine d'un nombre négatif.

je saute les étapes intermédiaires pour ne donner que les deux dernières :

alpha = ^3√(2-√-121) + ^3√(2+√-121)
alpha = ^3√(2-11√-1) + ^ 3√(2+ 11√-1)

Simplification
Le problème est que la solution obtenue ne semble pas très réelle. Nous allons essayer de la simplifier.

Calculer (2 + √−1)^3 et (2 − √−1)^3, en supposant que √−1 au carré = −1.

(
2+ √-1)^3 = 2^3 + 32^2√-1 + 32(√-1)^2 + (√-1)^3
= 8 + 12√-1 -6 -√-1
= 2+ 11√-1
pour (2-√-1)^3 = 2 - 11√-1

donc 2+√-1 = ^3√2+11√-1
et 2-√-1 = ^3√2-11√-1
2. Simplifier alors la solution obtenue. Que constate-t-on ? Vérifier que la solution réelle obtenue
est bien solution de l'équation x3 − 15x − 4 = 0.

l
a solution obtenue peut alors être simplifiée par alpha = 2-√-1 + 2 + √-1 = 4

vérifions : 4^3-15*4-4=0
64-60-4=0
donc 4 est bien la solution de x^3-15x-4

J'espère que vous pourrez m'aider là où je n'ai pas réussi et que vous pourrez me corriger. Je vous remercie d'avance pour le temps que vous prendrez à lire tout cet exercice et à me répondre.

<img src="http://www.mathforu.com/transfertfichier/fichiers/1712-
fichier-math.png" alt="fichier math"title="fichier math">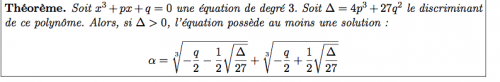 $fichier math$

Bonsoir barca,

Pour la question 2, étudie les variations de la fonction et utilise le théorème des valeurs intermédiaires.

Bonjour.
Je laisse Noemi s'occuper de toi, mais j'interviens juste pour te signaler que si l'aspect historique du problème t'intéresse, tu peux cliquer sur le lien suivant : Equation du troisième degré dans R.
Bonne lecture.

Merci à vous deux, pour vos réponses rapides.
Noemi, merci j'ai réussi la question 2 du 1)
Je bloque maintenant sur le 2. du 2) car je ne vois pas comment je peux trouver 3 réels alpha, bêta, gamma, du moins je ne sais pas par ou commencer.

En l'absence de Noemi :
Pour f(x) = x³ - 15x - 4
As-tu calculé f(-√5) ? quel est son signe ?

Bonjour à Mathtous, Noemi et Narca ,

Barca , pour te permettre d'avancer en attendant que Noemi soit là , je te donne une indication pour le 2 du 2)

C'est exactement le même principe que pour le 2 du 1)

Tu as étudié les variations de f

Utilise 3 fois le théorème des valeurs intermédiaires : une fois sur ]-∞,-√5] , une fois sur [-√5, √5] et une fois sur [√5,+∞[
Sur chacun de ces intervalles , tu prouveras que l'équation f(x)= 0 a une unique solution.
Au total : tu obtiendras donc 3 solutions α , β , γ.

( l'énoncé ne te demande pas ici les valeurs exactes ou approchées des solutions , mais seulement leur existence )

Remarque : si tu veux bien réaliser : trace la courbe sur ta calculatrice : cette courbe coupe l'axe des abscisses en 3 points ( ces abscisses étant α , β , γ )

Moemi continuera de t'aider lorsqu'elle sera là .

PS : Je bien de me rendre compte qu'à la question 1)3 , la valeur de alpha n'est pas bonne. c'est peut-être une faute de frappe :α≈-2.094

( Bonjour Mathtous . Je n'avais pas vu ta réponse...)

Merci beaucoup pour ton aide! J'ai enfin compris, et ce n'était en fait qu'un léger oubli dans mon cerveau.

Merci également pour le -2,094 j'ai en effet fait une faute de frappe à la calculatrice

Je pense maintenant avoir tous les conseils nécessaires pour terminer cet exercice et je vous en remercie.