DM : les suites
-
AAdibou dernière édition par
Bonsoir,
A peine repris que je bloque déjà sur mon premier exercice de maths, j'ai du mal a démarrer, alors si quelqu'un pourrez m'aider s'il vous plait, merci d'avance !Exercice:
Dans un repère orthonormé (O, i , j) on définit la suite de points A0 , A1 , A2 , …, An … de telle sorte:
A0 est le point de coordonnées ( 1,0)
pour tout entier naturel n≥ 1, le triangle OAnAn+1 est direct, rectangle et isocèle en AnI) Figure
Avec une échelle de 1 unité = 10 cm faire une figure sur laquelle vous placerez les dix premiers points A0, A1, A2.... A9II) Etude de la suite (Rn)
Pour tout n ∈ N on pose Rn=OAn, on a donc r0=OA0=1- Représenter r0 et r1 sur la figure puis calculer r1
- En vous plaçant dans le triangle OAnAn+1 montrer que Rn+1=(1/√2)Rn
En déduire la nature de la suite (Rn) et préciser ses éléments caractéristiques - Déduire de la question précédente l'expression de Rn en fonction de n
J'ai commencé seulement par placer mon point A0, je ne vois pas comment calculer les coordonnées de A0, A1, A2 ... etc ainsi qu'où se trouve le point An ?
Merci beaucoup, bonne soirée.
-
Bonjour Adibou,
L'énoncé c'est n ≥ 1?
Le triangle OAOAOA_0A1A_1A1 est rectangle isocèle en A0A_0A0.
Comme tu as placé O et A0A_0A0, tu peux placer A1A_1A1.
et ainsi de suite
-
AAdibou dernière édition par
Bonjour,
Oui c'est bien ça,
J'ai commencé a placer mes points, ça me donne ça, c'est correct ?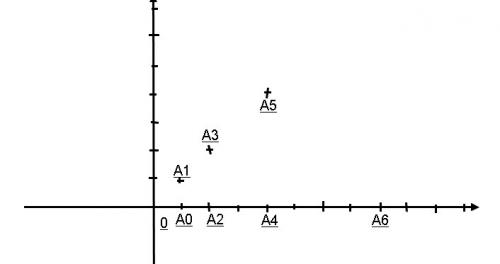
Mais pour le II) je bloque, r0 correspond à A0 et r1 est bien la longueur 0A1 ? du coup je trouve r1=√2 mais c'est faux.Merci
-
Pour la construction, tu n'as pas tenu compte du fait que le triangle est direct.
C'est rectangle isocèle en An ou An+1 ?
-
AAdibou dernière édition par
Il n'est pas direct ? mince c'est tout faux du coup,
Rectangle isocèle en An, A1 aurait du etre aux coordonnées (0;1) ?
-
Les coordonnées du point A1 sont-elles données dans l'énoncé ?
car le triangle direct débute pour n ≥ 1 !
-
AAdibou dernière édition par
Non, j'ai juste les coordonnées du point A0
Tout mes points sont faux donc ? je vois pas du tout ou pourrai etre A1
-
A1 serait bien placé si on considère que OA0A1 est direct et rectangle isocèle en A0, mais r1 = √2r0 ce qui ne correspond pas à le relation donnée à la question 2) !!
Vérifie l'énoncé.
-
AAdibou dernière édition par
J'ai vérifié, l'énoncé est bon
Je ne vois pas comment on peut arrivé a cette relation de l'énoncé, j'ai tout essayé...
-
As tu rectifié la figure ?
Tu arrives à la relation Rn+1 = √2 Rn
-
AAdibou dernière édition par
Non, je dois positionner A1 où ? désolé j'ai du mal ^^
Mais on doit arriver a Rn+1=(1/√2)Rn
-
Ce ne serait pas OAnAn-1 est direct ?
-
AAdibou dernière édition par
Mais c'est comment un triangle direct en fait ?
-
Si tu suis les lettres, tu tournes dans le sens des aiguilles d'une montre (Comme le cercle trigonométrique)
-
AAdibou dernière édition par
D'accord, merci, j'ai refait, mais c'est toujours pas ça je crois
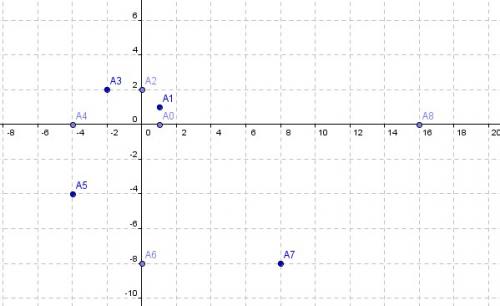
Mais j'ai le même problème pour r1 je trouve toujours √2 alors que je devrais avoir 1/√2
-
A mon avis il y a une erreur dans l'énoncé,
c'est le triangle OAnAn-1 est direct, rectangle isocèle en An.Refais la figure avec cet énoncé.
-
AAdibou dernière édition par
Oui ça semble bizarre, peut-etre que l'erreur est dans la relation, je vais mettre Rn+1=√2 R0 tant pis
c'est une suite géométrique ?
-
AAdibou dernière édition par
J'ai juste oublié de mettre la fin de l'exercice, que je n'arrive pas non plus à faire finalement
IV)
A l'aide d'un algorithme en langage naturel déterminer le plus petit entier naturel n0 à partir duquel An0 appartient au disque de centre O et de rayon 0,1 cmV) An sur les axes ?
- Déterminer les valeurs de n pour lesquelles An est sur l'axe des abscisses
- Déterminer les valeurs de n pour lesquelles An est sur l'axe des ordonnées
Je vois pas comment réaliser cet algorithme...