Pendule de FOUCAULT

Bonjour a tous,
J ai un probleme avec un dm a rendre lundi.
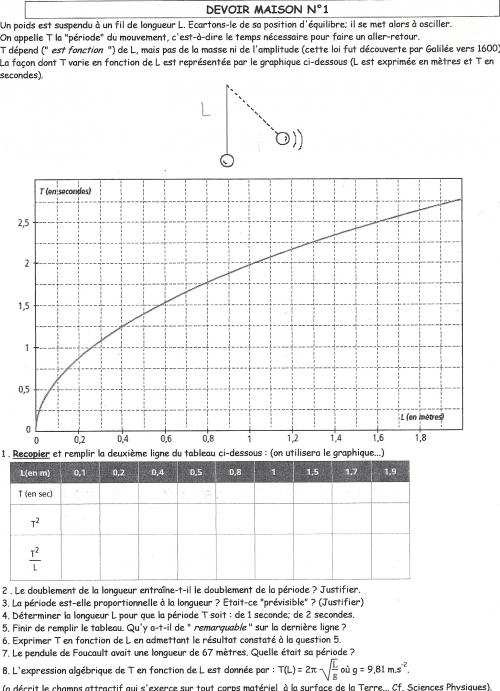
voila l'enonce:

Un poids est suspendu à un fil de longueur L. Ecartons-le de sa position d'équilibre; il se met alors a osciller. On appelle T la "periode" du mouvement, c est a dire le temps necessaire pour faire un aller-retour. T depend de L, mais pas de la masse ni de l'amplitude. La facon dont T varie en fonction de L est representee par le graphique ( L est exprimee en mètres et T en secondes).

P.S: est ce que je peux faire un scan pour vous montrer le graphique et le tableau qui va avec ?

recopier et remplir la deuxieme ligne du tableau ( on utilisera le graphique )
Le doublement de la longueur entraîne t il le doublement de la periode ? Justifier
La periode est elle proportionnelle a la longueur ? Justifier
Determiner la longueur L pour que la peride T soit: de 1 sec; de 2 sec
finir de remplir le tableau. Qu'y a t il de "remarquable" sur la derniere ligne?
Exprimer Ten fonction de L en admettant le resultat constaté a la question 5
Le pendule de foucault avit une longueur de 67 metres. Quelle etat sa periode?
L'expression algebrique de T en fonction de L est donnée par : T(L)=2pi√L÷g où g=9.81 m.s ^ -2

Merci par avance !

Bonjour momona,

Indique tes éléments de réponse et la question qui te pose problème.

En premier est ce qu il faut que je fasse un calcul ou juste que je lise le graphique a la question 1 ?
Parce que si je dois utiliser le graphique ca ne sera forcement pas tres precis et je me demandais si cela ne generais pas lors de la question 5

Question 1, c'est une lecture graphique.

ok merci. Bon c est a partir de la question 2 que je galere vraiment...

Analyse les résultats obtenus dans le tableau.

Non car par exemple pour 0.4 m:
0.4m = 1.25 sec.
1.25 × 2 = 2.5 sec or 0.8 m = 1.75 sec

c'est ca ?

En fait pour la question 2 et 3 je sais le faire mais j aurais besoin d'aide pour le rediger comme il le faut .

Personne pour m'aider s'il vous plait ?

Rédige tes réponses et on t'indiquera si cela est correct ou non.

Non car par exemple pour 0.4 m:
0.4m = 1.25 sec.
1.25 × 2 = 2.5 sec or 0.8 m = 1.75 sec

c'est ca ?

Attention aux écrits :
0.4m = 1.25 sec. ce n'est pas égal
pour l = 0,4 m la durée d'une période est t = 1,25 s

ok donc :
2) Le doublement de la longueur n'entraine pas le doublement de la periode. Par exemple pour l=0.4 m la durée d'une période est t=1.25 s. Si on double L et P on obtient pour l=0.8 m la durée est d'une période est t=2.5 s.
Or pour l=0.8 m la durée réelle est d'une période est 1.75 s.

C est ca ?

C'est correct.

Ensuite question 3) :

Non la période n'est pas proportionnelle a la longueur. Cela était previsible car si le doublement de la longueur n'entraine pas celui de la période, il est impossible qu'elles soient proportionnelles .

c'est bien ca ?

Ensuite question 3) :

Non la période n'est pas proportionnelle a la longueur. Cela était previsible car si le doublement de la longueur n'entraine pas celui de la période, il est impossible qu'elles soient proportionnelles .

c'est bien ca ?

Calcule les rapports L/T.

3)Non la periode n'est pas proportionnelle la longueur. Par exemple pour L=0.1m la durée d'une période est T≈0.63 s. Si on multiplie par 4 L et T on obtient pour L= 0.4 m la durée d'une periode est T≈2.52 s. Or pour L=0.4 m la durée réelle est T≈1.25 s.
Cela était prévisible car si le doublement de lalongueur n'entraine pas celui de la période alors il est impossible que la période soit proportionnelle a la longueur.

C'est bon ?

C'est correct.

d' accord merci. En revanche je ne vois pas comment, a la question 4, je peux determiner la longueur L pour que la periode T soit de 1s et 2s.

Car vu que L et T ne sont pas proportionnelles je ne sais pas quelle calcul je dois faire. A moins qu il faut que j'utilise le graphique?

Question 4, utilise le graphique.

d'accord. alors
4) D'apres le graphique on a:
pour t=1s, la longueur approchée est L ≈0.25 m
pourT=2s, la longueur approchée est L≈1 m

5 Apres avoir effectuer les calculs, on trouve dans la dernière ligne:
≈3.97 pour L=0.1m
≈3.96 pour L= 0.2 m
≈3.9 pour L=0.4 m
≈3.97 pour L=0.5 m
≈3.96 pour L=0.8 m
≈3.96 pur L= 1m
≈3.96 pour L=1.5 m
≈3.97 pour L=1.7 m
≈3.98 pour L= 1.9 m
On remarque que le resultat est presque toujours ≈4

C'est bon ?

Ensuite 6):

T(L)=T²/L≈4

la je n'en suis pas sur , c'est ca ?

C'est correct, cela dépend de la précision de la lecture du graphique.

la question 6) aussi est correct ?

T(L)=T²/L≈4

La période du pendule de foucault =
67/4≈16.75 s

c'est bon ?

personne pour me repondre ? Je suis vraiment perdu ...

7 faux
T² = 4L
soit T = ...

T²=4L
soit T=2L

c'est bon ?

P.S: est ce que la question 6 est exacte ?

Non

T² = 4L
donne puisque T ≥ 0
T = √(4L)
= 2√L

Donc:
6) on a:
T²=4L
T=√(4L)
T= 2√L

Par contre j ai pas comprs le "puisque T ≥ 0" ?

La période du pendule de Foucault = 2√67
≈16.4 s

c'est ok ?

C'est juste.

Mathématiquement T² = 4L admet deux solutions T = 2√L et T = -2√L

Comme T ≥ 0, T = 2√L.

super merci.
Maintenant pour finir la question 8:

L'expression algebrique de T en fonction de L est donnée par : T(L)=2pi√L÷g où g=9.81 m.s ^ -2
Recopier et completer l'algorithme suivant: (une seule opération par etape exigée).
Entrée: longueur L
Traitement:
Sortie: valeur de T

Donc j'ai trouvé:

L/g≈ 16.37/ 9.81 ≈ 1.67
√1.67≈1.29
2pi × 1.29 ≈8.1

donc T≈8.1 s

c'est bon ?

le g est sous le radical ?

Si c'est le cas, le résultat est correct.

oui ... enfin je crois ! Si tu pouvais verifier sur le scan parce que je sais pas trop ce que c'es le radical ...

Oui,

le g est sous le radical,
ton calcul est juste.

merci beaucoup de ton aide et surtout de ta patience !