Calculer la mesure d'un angle

Bonjour à tous,
Alors voilà j'ai un DM de maths à rendre le lundi 8 octobre et je n'arrive vraiment pas à résoudre l'exercice n°2 que voici:

"Quatre segments [AB], [BC], [CD] et [DE] de même longueur sont placés de telle sorte que D est sur la demi-droite
[AB), C appartient au segment [AE] et ADE est un triangle rectangle en D. Calculez la mesure exacte de l’angle de
sommet A."

J'ai réussi à tracer la figure pour AB=BC=CD=DE=3.2cm pour AD=8cm.
Le problème c'est qu'apres plusieurs pistes de recherche, je n'arrive toujours pas à trouver la valeur EXACTE de l'angle A (je n'arrive qu'à des valeurs approchées)...

Si quelqu'un pourrais m'aider ce serait génial!
Merci d'avance pour toute aide.

Bonjour,

Tu as recopié ton énoncé tel qu'on te l'a donné ? Parce que je le trouve particulièrement pas clair ... Donne l'énoncé complet s'il-te-plaît.

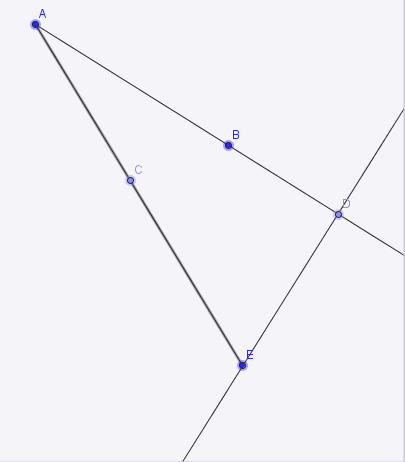
Donc la figure ressemble à ça ?

mesure d'angle

Bonjour,
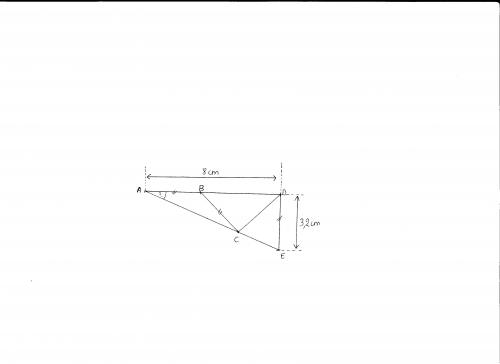
J'ai recopié l'énoncé mot pour mot et au complet, mais la figure n'est pas exactement comme cela.
En fait, on obtient un triangle rectengle en D avec [DE]=3.2cm ; (DA] = 8cm et DB = 3.2cm.
Et c'est là que votre figure diffère de la mienne; à savoir que [BC]=[DC] c'est à dire 3.2cm (le point C est donc plus proche du point E que du point A).
De plus, il faut tracer les segments [BC] et [CD].

Bonjour,

Si tu as la figure , tu peux la mettre ( regarde au dessous du cadre texte "
Ajoute une image" ( mets seulement la figure , pas de texte ! )

figure un peu petite pas facile à voir mais enfin...(je ne mets pas les chapeaux sur les angles.)
BAE+DEA=90°
EDC isocèle donc AED=ECD
ABC isocèle donc BCA=CAB
par suite
ACB+ECD=DAE+AED=90
Doù BDC =90
BCD isocèle rectangle donc CBD=BDC=45
mais CBD=BAC+BCA (angle extérieur)
finalement CAB=CBD/2= 22°30' ou π/8

ouf !

Merci à ceux qui m'ont apporté leurs aide. J'ai finalement trouvé grâce à une amie.