DM (fonctions)

[bouli1407]

Bonjour,
Quelqu'un peut-il me dire si ce que j'ai fait est juste ?

ABC est un triangle isocèle en A, avec AB=AC=7cm et BC=9cm
Sur le segment [AB], on place un point M quelconque. La parallèle à (BC) passant par M coupe [AC] en N.
On note $x$ la distance AM.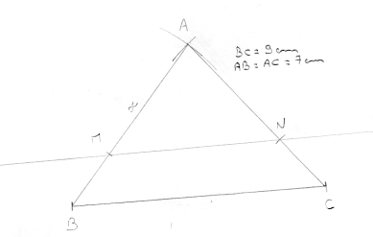

1. A quel intervalle I, $x$ appartient-il ?

$x$ ∈ ∈[0 ; 7]

2. Soit p la fonction qui à tout $x$ de I associe le périmètre du triangle AMN
   a) Exprimer AN et MN en fonction de $x$ (utiliser le théorème de Thalès)

**D'après Thalès, j'ai : $\frac{x}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ donc $\frac{x}{7}=\frac{AN}{7}=\frac{MN}{9}$ donc.... $AN=\frac{7x}{7}=x$ et $MN=\frac{9x}{7}$

b) En déduire $p(x)$ en fonction de $x$
p = périmètre de AMN = AM+MN+AN**

$p(x)=x+\frac{9x}{7}+x=2x+\frac{9x}{7}=\frac{14x+9x}{7}=\frac{23x}{7}$

c) La fonction pp est-elle une fonction que vous connaissez ?

Si $x=0$ alors p(x)=0 La fonction p passe donc par l'origine du repère, c'est donc une fonction linéaire

d) Représenter graphiquement le fonction p sur I

Pas de souci particulier....

e) Déterminer graphiquement pour quelles valeurs de $x$ le périmètre $p(x)$ est strictement supérieur à 11.5 cm (faire apparaître les traits de construction)

Sur mon graphique, j'observe que $p(x)$>11.5 à partir du moment où $x$>3.5

3. Soit $q$ la fonction qui à tout $x$ de I, associe le périmètre du trapèze BMNC.
   a) Exprimer $q(x)$ en fonction de $x$

**$q(x)$=périmètre de BMNC=MB+BC+NC+MN

MB=NC=$7-x$
BC=$9$
MN=$\frac{9x}{7}$**

donc $q(x)=2(7-x)+9+\frac{9x}{7}$=$=14-2x+9+\frac{9x}{7}=23-2x+\frac{9x}{7}=23-\frac{14x+9x}{7}=23-\frac{5x}{7}$

b) La fonction $q(x)$ est-elle une fonction que vous connaissez ?

Si $x=0$, $q(x)$≠0 Donc, $q(x)$ ne passe pas par le centre du repère, donc $q(x)$ est une fonction affine

Voilà où j'en suis.
Il reste encore deux questions, mais avant d'aller plus loin, j'aimerais être sur que ce que j'ai fait jusque là est juste. Notamment pour les calculs......
Quelqu'un peut-il me rassurer ou éventuellement corriger mes erreurs ?

Merci d'avance

[Noemi]

Bonjour bouli1407

Pour le début, les résultats sont justes.
Une erreur dans l'écriture de q(x) 23 - 2x + 9x/7 = 23 +(-14x+9x)/7
= 23 - 5x/7

[bouli1407]

Ok, ça expliquerait donc pourquoi ça ne colle pas ensuite pour la suite de l'exercice....

Mais alors, à quoi est égal q(x) ?

J'avais fait un premier calcul qui me donnait : q(x)= 23 - 23x/7 qui collait pour la suite de l'exercice, mais, en refaisant mes calculs, je trouvais que ce résultat était faux....

[Noemi]

Le résultat obtenu pour q(x) est juste.

Poursuis l'exercice.

[bouli1407]

quel résultat est juste ? 23 - 5x/7 ?

[Noemi]

Oui

q(x) = 23 - 5x/7

[bouli1407]

Suite de l'exercice:

3. c) Représenter graphiquement la fonction q sur le même graphique que p

Pas de souci particulier

4. Pour quelles valeurs de x, AMN et BMNC ont-ils le même périmètre ? (répondre graphiquement en expliquant comment vous faites puis à l'aide d'un calcul)

Sur le graphique, je constate que les représentations gaphiques des 2 fonctions se coupent en un point d'absisse 5.75 C'est donc la valeur de x pour laquelle les périmètres de AMN et BMNC sont égaux.

Je résouds ensuite l'équation p(x) = q(x) et j'obtiens 23/4 qui est égal à 5.75 Donc, pour moi, tout va bien ! Quand x=23/4, les deux périmètres sont égaux

Cependant, un petit truc me chiffonne : dans l'énoncé, on me demande de trouver "LES valeurs pour lesquelles....etc...." Et moi, je n'en trouve qu'une. Est-ce un petit piège ? ou bien, ai-je loupé quelque-chose ?

[Noemi]

Non, pas de piège, une seule valeur possible pour x.

[bouli1407]

Je peux donc dire à mon prof qu'il y a une erreur dans l'énoncé : valeurs au pluriel.... ? Mais non, je m'amuse !

Merci en tout cas de m'avoir consacré un peu de votre temps !