Réaliser l'étude complète d'une fonction avec exponentielle

Bonjour, j'aurais besoin d'aide pour cet exo, merci.

Partie A
Dans un repère orthonormé (O,i,j) on a tracé deux courbes C1 et C2.
L'une représente une fonction f dérivable sur R et l'autre représente sa dérivée f'.
le point A de la courbe C2 et les points B et C de la courbe C1 ont des coordonnées entières.
Associer à chaque fonction sa courbe en justifiant la réponse.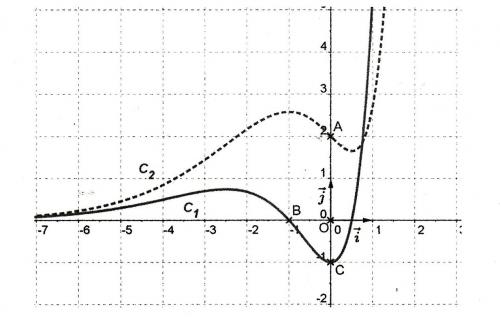

$fichier math$

Partie B
Soif f la fonction définie sur R par f(x)=(ax²+bx+c)e puissance ×
où a, b et c sont des nombres réels.

Calculer f'(x) en fonction de a, b et c.
2.a. Justifier, à l'aide des données graphiques, que a=2, b=-3 et c=2
b. Écrire alors les expressions de f(x) et f'(x).
Faire le tableau de variation de f en justifiant la réponse
Déterminer le signe de f(x), justifier.
Déterminer une équation de la tangente TA et C2 au point A puis tracer TA.

Bonjour Ju',

Indique tes éléments de réponse et la question qui te pose problème.

A Analyse les variations.

Merci, alors pour la 1. J'ai calculé f'(x) qui est de la forme u*v
Avec u=ax²+bx+c v=e^x (soit la fonction exponentielle)
u'=2ax+b v'=e^x
donc f'(x)=(2ax+b)*e^x+(ax²+bx+c)*e^x
=(2ax+b+ax²+bx+c)*e^x
=(ax²+(2a+b)x+b+c)e^x
C'est simplement ça pour la question 1?

Pour la partie A je ne vois pas comment faire.

Si on connait le signe de la dérivée d'une fonction, on en déduit le sens de variation.

sur l'intervalle ]-7 ; -1],
C1 est positive ou négative ? croissante ou/et décroissante ?
C2 est croissante ou décroissante ? Positive ou négative ?

C1 est positive sur ]-7;-1]u[0.5;1[
Croissante sur ]-7;2.5]u[-1;1]
C2 est positive et est croissante sur ]-7;-1]u[0.5;1]
Mais je me suis aidée du graphique donc ce n'est pas précis

C2 est toujours positive, donc si C2 était la représentation de la fonction dérivée, C1 serait toujours croissante ou décroissante ?

C1 serait toujours croissante

Oui,

donc .....

Donc C1 est la dérivée

Vérifie les variations de C2 à partir du signe de C1.

si la dérivée d'une fonction est négative sur un intervalle, alors la fonction est décroissante sur cet intervalle.
De plus C1 est négative sur [-1;0.5] et C2 est décroissante sur [-1;0.5]

si la dérivée d'une fonction est positive sur un intervalle, alors la fonction est croissante sur cet intervalle.
C1 est positive sur ]-7;-1]u[0.5;1[ et C2 est croissante sur ]-7;-1]u[0.5;1[

On peut en conclure que C1 est la dérivée de f.

C'est correct.

Ju'
Merci, alors pour la 1. J'ai calculé f'(x) qui est de la forme u*v
Avec u=ax²+bx+c v=e^x
u'=2ax+b v'=e^x
donc f'(x)=(2ax+b)*e^x+(ax²+bx+c)*e^x
=(2ax+b+ax²+bx+c)*e^x
=(ax²+(2a+b)x+b+c)e^x
C'est simplement ça pour la question 1?

La dérivée est juste.

D'accord, pour la 2.a je trouve bien a=2 c=2 mais comment fait on pour trouver b?

Tu utilises le point C, soit f'(0) = -1

Je te remercie de ton aide, ça y est, j'ai fini l'exercice
Juste une dernière question g(x)= x e^-x +2
g est de la forme u*v ou u+v?

Des deux formes
$xe^x$ forme u*v