Section d'un cube

Bonsoir à tous !

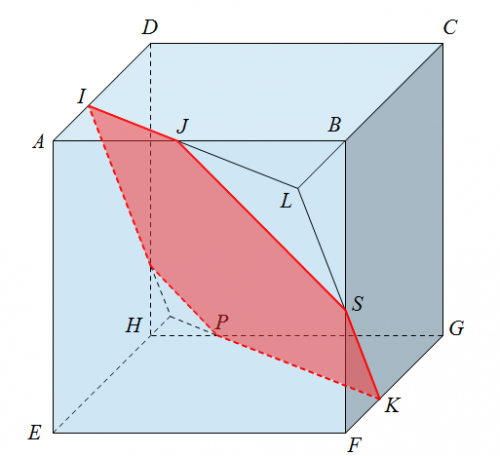
J'ai un exercice qui consiste en la réalisation de la section d'un cube. Il s'agit d'un cube ABCDEFGH avec I,J et K qui sont des points appartenant respectivement aux segments [AD],[AB] et [FG]. Il faut faire la section de ce cube par le plan (IJK).

Voila ce que j'ai fait : J'ai tracé l'intersection de (IJK) par la face ABCD , il s'agit de [IJ] . J'ai fait de meme avec la face EFGH il s'agit de [PK](avec P un point qui coupe le segment [HG]). Par contre a partir de ce moment-là , je ne sais plus quoi faire. Notre professeur nous a donné une petite aide en nous demandant de justifier le fait que (KL) et (BF) sont sécantes en un point, mais je ne voit vraiment pas comment faire.

Merci d'avance pour votre aide !

Bonjour,

l'idée ici est de "sortir du cube" : prolonger certaines arêtes pour trouver leurs intersections avec le plan (IJK).
On peut aussi utiliser le parallélisme : les faces parallèles seront coupées selon des droites parallèles. C'est le cas de (IJ) et (PK) normalement.

Je te conseille de faire un dessin avec plusieurs couleurs : une pour le cube, une pour la section cherchée, et une autre pour les parties qui "sortent" du cube.

Tu peux joindre une image de ce que tu as fait, ce sera plus facile pour expliquer.

Merci beaucoup pour votre réponse ! Oui oui sans problème!

Malheureusement on ne voit pas les noms des points !
Edit : bon avec l'énoncé et un peu de devinette, j'y arrive.

Donc tu as bien (IJ)//(PK), c'est bien.
Le parallélisme ne te permet pas de continuer, c'est maintenant qu'il faut sortir du cube.
J'ai un exemple sur un autre cube, ça montre le principe :

$fichier math$

Ma face du dessus correspond à ABCD et celle du bas à EFGH avec I un point de [AD], J point de[AB] et K point de [FG].
J'ai tracé un point L intersection de (IJ) et (BC) et un point S intersection de (KL) et (BF) (par contre je ne sais pas comment justifier qu'elles sont sécantes) . J'obtiens IJSKP section du cube. Cela est il juste ?

• J'ai tracé un point L intersection de (IJ) et (BC) et un point S intersection de (KL) et (BF) ✓

• (par contre je ne sais pas comment justifier qu'elles sont sécantes) .
→ droites sécantes = droites coplanaires et non parallèles. C'est le fait qu'elles soit coplanaires qui importe ici.
Quel plan contient à la fois K, L, B et F ?
Ce plan contient aussi les deux droites (KL) et (BF).

• J'obtiens IJSKP section du cube. Cela est il juste ?
→ Tu as le début (la partie avant) mais il te manque un point à l'arrière du cube : pour finir la section on ne peut pas faire le segment [PI] car P et I ne sont pas sur la même face du cube.
Tu dois faire avec (KP) et I exactement la même chose qu'avec (IJ) et K.
C'est juste un peu plus dur à voir car c'est à l'arrière.