Etudier la fonction aire de l'espace hachuré

bonjour a tous
pouvez vous m'aider au sujet de cet exercice

ABC est un triangle rectangle en A tel que AB =4 et AC=2
M étant un point mobile sur AB, on désigne par x la longueur CM. La parallèle à AB passant par M coupe BC en P et la La parallèle à AC passant par P coupe AB en Q

1a)Exprimer le longueur MP en fonction de X Justifier de façon précise
b)Exprimer l'aire du rectangle AMPQ en fonction de x
c)En déduire que l'aire hachuré f(x)est égale a 2x²-4+4
2)montrer que f(x)=2(x-1)²+2pour toux x
3)a)montrer que f est croissante sur [1;∞[ et décroissante sur ]-∞;1]
b)interpréter géométriquement ces résultats (pour l'aire hachure)

merci d'avance

Bonsoir mllschoe,

Vérifie l'énoncé
M appartient à (AB) et la parallèle à (AB) passant par M !!

Indique tes éléments de réponse.

oui desoler je me susi troper c'est M étant un point mobile sur AB, on désigne par x la longueur( CM)

j'ai appliquer thales et donc MP/BA = x/CA MP= BA.x/C
l'aire du rectangle = AM.MP = AM.(BA.x/CA) = -2x²+4

C'est M appartient au segment [AC] !!!

1 juste
2 vérifie le calcul, il manque un x

(CA-x)(BA.x/CA)= -2x²-4x
pour c) j'ai fait Aire triangle = (ACAB)/2 - aire rectangle = -2x+4x
(ACAB)/2 -2x+4x
4-2x+4x
apres pour la suite je ne comprend pas

b) C'est 4x - 2x²
c) L'aire hachurée correspond à quoi ?

voici la figure [

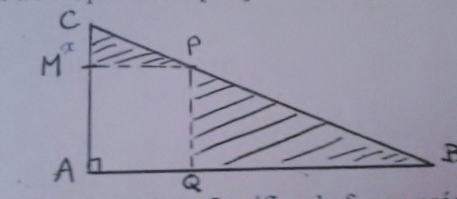
$fichier math$

Refais le calcul pour l'aire hachurée.

la je suis perdu je ne comprend pas

Calcule :
l'aire du triangle ABC : ...
l'aire de la partie hachurée : ....

et le 2) comment je fait pour montrer quef(x)=2(x-1)²+2 pour toux x ?

Développe cette expression.