Résolution de problème en s'aidant du cercle trigonométrique

bonjour j'ai fais la premiere partie mais je suis bloqué a la deuxieme

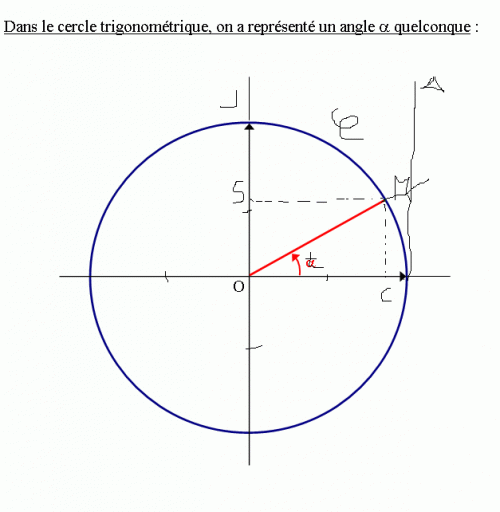
$fichier math$
sur la figure ci dessus M est un point du cercle trigonometrique C tel que la mesure t de l'angle oriente (OI , OM)en radians appartienne a (0; pi/2)
C et S sont les projetes orthogonaux du point M sur les axes du repere (O,I, J)
T est le point d'intersection de la droite (OM) et de la droite tangente delta au cercle C en I
1a) donner en fonction de t :
les coordonnes de M C et S
le coefficient directeur de (OM)
b) écrire l'équation de la droite (OM) et en déduire que les cordonne T sont (1; sint/cost)
c) calculer en fonction de t la distance IT
2a) precisez la nature du triangle OIM puis exprimer son aire A1 en fonction de t
b) expimer l'aire A3 de OIT en fonction de t
c) le secteur angulaire OIM est la partie du plan comprise entre les segments (OI) et (OM) et l'arc de cercle IM.
on rapelle que l'aire d'un secteur angulaire de rayon R et d'angle au centre l est égale a 1/2lr²
déterminer l'aire A2 du secteur angulaire OIM en fonction de t

J'ai trouvé pour le 2)a) qu'il est quelconque mais je ne sais pas le prouver

Bonjour,

2)a) .

Le triangle OIM est isocèle car OI=OM

En utilisant la formule usuelle de l'aire d'un trianglr :

$\text{aire(oim)=\frac{oi \times cm}{2}=\frac{oi\times os}{2}=\frac{1\times sint}{2}=\frac{1}{2}sint$

mtschoon
Bonjour,

2)a) .

Le triangle OIM est isocèle car OI=OM

En utilisant la formule usuelle de l'aire d'un trianglr :

$\text{aire(oim)=\frac{oi \times cm}{2}=\frac{oi\times os}{2}=\frac{1\times sint}{2}=\frac{1}{2}sint$
Bonjour comment on sait que OM=OI?

OI et OM sont deux rayons du cercle ( OI=OM=1 , vu que le cercle trigonométrique a pour rayon 1 )

mtschoon
OI et OM sont deux rayons du cercle ( OI=OM=1 , vu que le cercle trigonométrique a pour rayon 1 )
A oui c'est vrai il est trigonométrique
Pour le 2 j'ai trouvé OI×IT/2=1×sint/cost /2= sint/cost /2
c'est ca?

ton écriture est un peu confuse mais je pense que tu as la bonne réponse :

$\text{aire(oit)=\frac{1}{2}\frac{sint}{cost}=\frac{sint}{2cost}$

mtschoon
ton écriture est un peu confuse mais je pense que tu as la bonne réponse :

$\text{aire(oit)=\frac{1}{2}\frac{sint}{cost}=\frac{sint}{2cost}$
oui c'est sa
par contre le 3) je ne sais pas

eragny
mtschoon
ton écriture est un peu confuse mais je pense que tu as la bonne réponse :

$\text{aire(oit)=\frac{1}{2}\frac{sint}{cost}=\frac{sint}{2cost}$
oui c'est sa
par contre le 3) je ne sais pas
La c) je me suis trompé

Pour l'aire du secteur circulaire OIM , applique la formule qui t'ai donnée.

Ici , l =t et r=1

mtschoon
3) ?

Tu parles peut-être de la question 2)c) ?

Pour l'aire du secteur circulaire OIM , applique la formule qui t'ai donnée.

Ici , l =t et r=1

1/2t1²
c'est ca?

je suis pas sur

Oui , mais 1²=1

Donc l'aire cherchée s'écrit $12t=t2\frac{1}{2}t=\frac{t}{2}$

mtschoon
Oui , mais 1²=1

Donc l'aire cherchée s'écrit $12t=t2\frac{1}{2}t=\frac{t}{2}$
y'a pas besoin de mettre le t?

relis ma réponse...il y a bien le "t" ...

mtschoon
relis ma réponse...il y a bien le "t" ...
Je l'avais pas vue
Merci de m'avoir aidé

De rien !

Bonjour je suis en $1^{ere}$ :frowning2: et je n'y arrive pas dut tout a ce Devoir Maison si quelqu'un pourrait m'aider svp juste a me donner les coordonnées des trois points svp :frowning2:

Bonjour,

M a pour coordonnées (cost,sint)

C a pour coordonnées (cost,0)

S a pour coordonnées (0,sint)

merci beaucoup

donc pour le coefficient directeur (yM-yO)÷(xM-xO)=sint÷cost non ?

exact.

Rebonjour j'aurai une petite question pour le 3 puisque je n'y arrive pas
Comment devons nous faire pour comparer les trois aires ?

Dans l'énoncé écrit , je ne vois pas de question 3) , alors écrit cette question 3) en totalité .

a) On admet A1≤A2≤A3.Déduire des questions précedentesque , pour tout t de [0;∏/2]: tcost≤tsint≤t

b)à l'aide de l'encadrement obtenu,montrer que pour tout réel t de [0;∏/6] 0.86t≤sint≤t .

Tu as écrit :
Citation
tcost≤tsint≤t

Je te suggère de vérifier car , par exemple , pour t=∏/6 , c'est faux...

c'est exactement marqué comme ca dans mon livre de mathématiques
Je vien de revérifier

Pour que cette inégalité soit vraie , il faudrait que cost soit inférieur à sint .

Si tu choisis une valeur de t comprise entre 0 et ∏/4 , le cosinus est supérieur au sinus , donc ça ne va pas...