Trigonométrie ; Angle associés 1erS

[Nessaah]

On considére la figure ci-dessous, dans laquelle R est le cercle de centre O de rayon 3, B un point de R tel que (OA OB ) = pi/4 OAB est rectangle en A et C est tel que (OA,OC) = pi/3

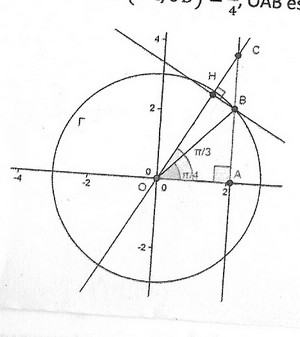
1- Déterminer les coordonnée de A, B et C
2 - En déduire la longueur BC
3 - a) On note H le projeté orthogonal de B sur (OC). En déterminant la mesure de(CO,ÇA), calculer HB
b) Déterminer la mesure de (OB,OC)
c) En raisonnant dans OBH déterminer alors les valeurs exactes de cos pi/12 et sin pi/12

[mtschoon]

BONJOUR ! ( un petit "Bonjour" fait plaisir )

Pistes pour démarrer ,

A a pour coordonnées (2 , 0)

B a pour coordonnées (2 , 2) ( le triangle OAB est rectangle isocèle )

C a pour abscisse 2

Dans le triangle rectangle OAC :

$\text{\tan\frac{\pi}{3}=\frac{ac}{oa}$

Donc : $\text{ac=oa\tan\frac{\pi}{3}=2\tan\frac{\pi}{3}$

Tu remplaces tan(∏/3) par sa valeur et tu obtiendras ainsi l'ordonnée de C

Essaie de poursuivre.