Déterminer graphiquement et algébriquement coordonnées des points d'intersection de segments et axes

Bonsoir ,

J'ai une question au sujet de cet exercice:

Dans un repère orthonormé, soient la points A(-2;3);B(-1/2;-3/2); C(3;-3/2);D(5;3/2) et E(9;-5/2) et f la fonction représenative de la ligne brisée ABCDE.

Construire la courbe Cf de cette fonction .
Déterminer graphiquement et par le calcul, les coordonées des points d'intersection respectifs F,G,H des segments [AB],[CD] et [DE] avec l'axe des abscisses .

Pour la première question c'est bon mais pour la deuxième je ne comprend pas ce que l'on me demande et comment procéder .
pouvez-vous m'aider ?

Cordialement

Merci

Bonjour,

il faut que tu trouves les equations associees aux segments [AB] [CD] et [DE]

rappel : equation d'une droite y=ax+b

mushki
il faut que tu trouves les équations associées aux segments [AB] [CD] et [DE].
Rappel: équation d'une droite $y = a x + b$ Bonjour

Voici les explications sur cette méthode pour trouver l'intersection du segment [AB] avec l'axe des abscisses [O, $x$ )

Soit le point $\cap [O,x)$

On sait que $y_M=0$ et on cherche à calculer $x_M$

Pour trouver l'équation de droite (AB) , il faut trouver les 2 nombres $m$ et $p$ tel que
$y_A=m x_A +p$
$y_B=m x_B +p$

Il faut donc résoudre un système de 2 équations à 2 inconnues

L'équation de la droite (AB) va te permettre de trouver le point M
c'est à dire de calculer $x_M$ car on a : $0=m x_M +p$

ps)
Attention: cette méthode permet de trouver un point $\in (AB)$
Ne pas oublier de vérifier / démontrer que ce point M appartient au segment [A,B]

Bonjour,

J'espère que tu as fait un graphique correct.
Tu peux ainsi "lire" les réponses demandées que tu les démontreras algébriquement ensuite.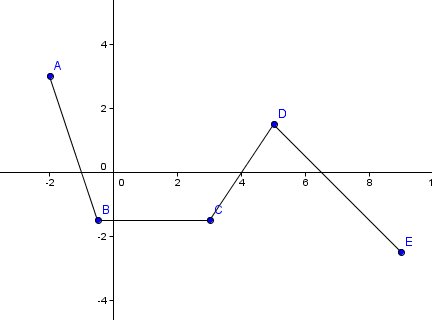

$fichier math$

Si tu as besoin , donne nous tes calculs et nous vérifierons.

Bonjour,

Merci pour votre aide .
Alors je trouve pour (AB): -9/2x-3/2Y-9/2=O soi le point F d'abscisse -1
pour (CD) je trouve : 3x-2y-12=O soit le point G d'abscisse 4
Et enfin (DC) : -4x-4y+26=O soit le point H d'abscisse 26/4 ou 6,5.

Je ne pense pas mettre trompée .

Merci

Bonjour,

Je regarde tes réponses :

Droite (AB) : c'est bon , mais tu peux simplifer.

Droite (BC ) ? ? à faire. c'est la plus simple ...

Droite (CD) : c'est bon

Droite (DE) : c'est bon , mais tu peux simplifier. ( tu as, je suppose , fait une faute de frappe en écrivant (DC) )

Comme il s'agit de segments ( en non de droites ) , indique la conditon sur x par exemple

Pour [AB] : -2 ≤ x ≤ -1/2 et indique que F convient car -2 ≤ -1 ≤ -1/2

(Fais pareil pour les autres segments )

Que veux tu dire par condition ?
Je ne comprend pas bien .

Merci

BC n'est pas demandée .

Si (BC) n'et pas demandée , tu n'as rien à faire..dommage...

Explication pour le segment [AB]:

L'équation ( simplifiée) de la droite (AB) est 3x+y+3=0
Cette équation s'applique pour tout x de R

L'équation ( simplifiée) du segment [AB] est 3x+y+3=0
Cette équation s'applique seulement pour x compris entre -2 et -1/2

douce87
Que veux tu dire par condition ?
Je ne comprend pas bienSalut
Il y a une différence entre $\in (AB)$ et $\in [A,B]$

Est ce que tu comprends ?

Je pense avoir compris sur (AB) le point peut se trouver n'importe ou tandis que sur [AB] il se trouve obligatoirement entre xA et xB.
Dites moi si mon résonnement est juste .

Oui , ton raisonnement est bon.

Merci de ton aide mtschoon à bientôt je vais avoir peut d'autres exercices que ja vais peut etre pas bien saisir .

Merci encore .

De rien !

A+