Fonction paire et périodique

Bonjour me revoilà,

j'ai beaucoup de mal à comprendre les énoncés donc je viens encore demander votre aide .

Soit une fonction f, définie sur R et vérifiant les trois conditions suivantes :

f est paire
f est périodique, de période 4.
Le tableau de variation de f dur l'intervalle [-4;4] est donné de façon incomplète .

X -4 -2 0 2 4
FX 2 2
0

1°) Reproduire sur votre copie et completer ce tableau.
2°) Si x∈ [0,2] alors f(x)=-x+2
Tracer alors la courbe Cf reprèsentative de f sur l'intervalle [-4;4], en justifiant ce tracé, dans le repère orthonormé : (O,I,J) d'unité 1 cm.

Désolée je ne peux pas mettre les flèche mais de 2 à O elles est descendante et de 0 à 2 elle est montante .

Merci .

Bonjour,

Le tableau que tu donnes pour la condition 3) est vraiment trop confus...Je ne peux donc pas t'aider pour la question 1.

Piste pour la 2)

Je suppose que tu connais la définition de fonction paire.

Ayant la représentation graphique de f pour x appartenant à [0,2] , par symétrie par rapport à l'axe des ordonnées, tu obtiendras la représentation graphique de f pour x appartenant à [-2,0]

Je suppose que tu connais la définition de fonction périodique.

Ayant la représentation graphique de f pour x appartenant à [-2,0] , par une translation de vecteur $4I⃗4\vec{I}$ , tu obtiendras la représentation graphique de f pour x appartenent à [2,4]

De même , ayant la représentation graphique de f pour x appartenant à [0,2] , par translation de vecteur $−4I⃗-4\vec{I}$ , tu obtiendras la représentation graphique de f pour x appartenent à [-4,-2]

X -4 -2 0 2 4
FX 2 2
0

Une fleche décroisante de 0 ,2 à 0 et un fléche croissante de 0 à 4,2 je sais pas si tu comprends pas facile je n'ai pas de scanner .

MERCI

x-4 fx rien
x-2 fx rien
x0 fx 2
x2 fx 0
x4 fx 2

Une fleche décroisante de 0 ,2 à 2,0 et un fléche croissante de 0,2 à 4,2 je sais pas si tu comprends pas facile je n'ai pas de scanner .

MERCI

Bonsoir ,

Dis moi si je dis une bétise il faut que f soit paire et periodique en meme temps ou je confonds.

Merci

Les 3 conditions doivent être vérifiées donc f doit être à la fois paire et périodique.

Citation
X -4 -2 0 2 4
FX 2 2
0

Citation
x-4 fx rien
x-2 fx rien
x0 fx 2
x2 fx 0
x4 fx 2

Tout ceci est incompréhensible . Désolée !

Ok donc dejà je n'ai pas dit de bétise ; mais dois-je faire un calcul ou simplement mettre des chiffres car je n'ai pas d'equation .
Car le but de ce tableau et d'avoir une fonction paire et périodique si je ne me trompe pas .

Merci pour ton aide

Pour x appratenant à [0,2] tu dois utiliser f(x)=-x+2 : tu obtiens le segment [AB]

Ensuite , tu construis les autres segments en utilisant parité et périodicité comme je te l'ai indiqué dans mon premier message.

Pour que tu puisse vérifier , je te joins un schéma :

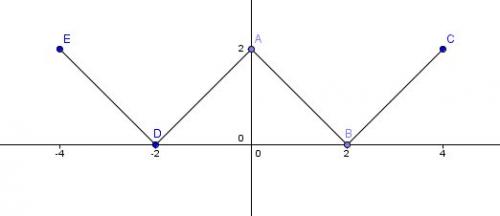
$fichier math$

YES C'est ce que j'avais trouvée dans le tableaux de variation mais j'avais un doute dans l'association des deux paire et periodique .

Merci

Ok pour la construction et le tableau de variation .
Moi je construit cette courbe à partir du tableau de variation mais on me demande de justifier ce tracé .

Bon je continue a chercher .

merci encore

Pour justifier le tracé , tu utilises ce que je t'ai indiqué dans mon premier message.

Avec f(x)=-x+2 pour x appartenant à [0,2] ( fonction affine ) , tu obtiens le segment [AB]

f paire : par symétrie par rapport à l'axe des ordonnées , [AB] ----> [AD]

f périodique de période 4 : [AD] --->[CB]

Tu termines comme tu veux ( périodicité ou parité )

Le plus simple à expliquer est peut-être la parité :

f paire : par symétrie par rapport à l'axe des ordonnées [CB]--->[ED]

merci mtschoon.

De rien.

A+