autre dm inequation

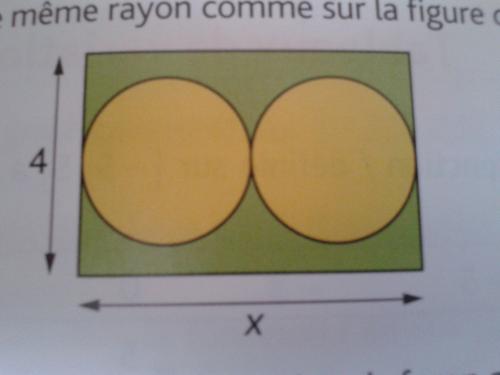
Soit un réel x dans l'intervalle [ 0; 8]. On considere un rectangle de dimension 4 cm sur x cm dans lequel on trace deux disques de meme rayons comme sur la figure si dessous $fichier math$

On souhaite determiner les valeurs de x de façon que la surface verte ait une aire supérieure ou égale a l'aire de la surface jaune

montrer que le problème se ramène a la résolution de l' inéquation : pi x ×² ≤ 16x sur [ 0·8]
Montrer que l'ensemble des solutions de linequation est [ 0; 16/pi]

Moi j'ai trouvée : air de la surface verte : 4x
Aire de 1 disque : 1/4× x pi²
Aire de 2 disque : 2/4× x pi²
Donc × x pi²

Mais apres je suis bloquée, sa serait gentille de m'aider
Merci de vos propositions

Bonsoir charlotte.h

Comment calcule t-on l'aire d'un disque de diamètre x/2 ?

Bonjour,
Ben on fais pi x (×/2)² ?

Non,

C'est π *(x/4)²

Ben oui c'est ce que j'ai mis non ?

Non, tu as mis x/2 !!

Non j'ai mis 1/4 de x donc c'est x/4

Simplifie 4x - 2*(π*(x/4)²) ≥ 2(π*(x/4)²)
....

je comprend pas là!
4x-2*(n*(x/4)²) sa represente quoi

Non j'ai rien dit sa représente la surface sans les disque jaune en faite

Non j'ai rien dit sa représente la surface sans les disque jaune en faite

Je n'arrive pas à simplifier tu peux le donner le début pour me mette sur la voie stp

4x - 2*(π*(x/4)²) ≥ 2(π*(x/4)²)
4x ≥ 4(π*(x/4)²)
x ≥ (π*(x/4)²)
x ≥ ....

donc ça fait
x ≥ n* x²*16
?

Un erreur πx²/16

D'ou l'inéquation du 1)

Ben non l'equation du 1 cest
Pi x ×²≥ 16x

Ce n'est pas la même chose

Tu as mis multiplier à la place de diviser.

D'acccccord!
Donc on obtient x ≥ n*x²/16

Mais il faut placer le 16 de l'autre côté mais si on le change de sens il va devenir négatif du coup sa ne fait plus la même inéquation ?

Si on multiplie une inéquation par un nombre positif, on ne change pas le sens de l'inégalité.