Problème ouvert dérivée : plus grand périmètre d'un triangle rectangle

Bonjour j ai un problème ouvert à résoudre et me voilà bloque..

Le problème est le suivant :
Parmi tous les triangles ABC rectangle en A tels que bc = 8 cm, y en a t-il qui a un périmètre plus grand que tous les autres ?

Mon travail est le suivant :

Utilisation de pythagore : ac= x. Bc = 8. Ac=y.
On en déduit que y = √(64-x²)

Le périmètre P est donc : x + √(64-x²) + 8

Calcul de la derivée de P. P'= 1 + (-2x)÷2√(64-x²)

Après cela je suis bloqué.. Merci de votre aide

Bonjour berlyn,

Etudie le sens de variation de la fonction.
Pour quelle valeur la dérivée s'annule ?

Bonsoir,

Pour étudier le sens de variation il faut que je simplifie p', je met sur le même dénominateur mais je bloque ensuite.. Pouvez vous m'aidez encore merci

Pour 0 < x < 8, tu résous l'équation :
x = √(64-x²)
si tu élèves chaque membre au carré cela donne
x² = ....

Cela donne x²=64-x² mais en quoi sa m'aide pour étudie le sens?

Merci d avance

Cela donne x²=64-x² mais en quoi sa m'aide pour étudie le sens?

Merci d avance

Résous cette équation, tu obtiens les valeurs qui annulent la dérivée.

Je met tout du même côté ce qui me donne accès à un calcul de delta sont les solutions sont :
-√512/4. Et. +√512/4

Cela est correct ?

Je met tout du même côté ce qui me donne accès à un calcul de delta sont les solutions sont :
-√512/4. Et. +√512/4

Cela est correct ?

Je met tout du même côté ce qui me donne accès à un calcul de delta sont les solutions sont :
-√512/4. Et. +√512/4

Cela est correct ?

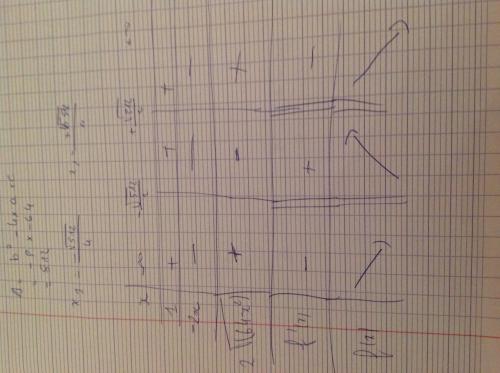
Mon tableau serait le suivant $fichier math$

L'équation est 2x²-64 = 0
ou 2(x²-32) = 0
les solutions sont -4√2 et 4√2
Or x compris entre 0 et 8, donc ....
puis tu construis le tableau de variation.

Bonsoir et encore merci de votre aide .
√512/4 ( valeur trouver avant ) est la meme chose que 4√2 ( merci pour la simplification )

Or dans le triangle rectangle l'hypoténuse est 8 cm donc x doit etre compris entre 0 et 8 ( 0≤x≤8)
Seule la solution 4√2 est donc possible

Ce qui nous donne le tableau de variation suivant :

Je ne comprend pas comment vous arrivez directement sur : x = √(64-x²)
alors qu'on avait la dérivée : P'= 1 + (-2x)÷2√(64-x²) qui semble ne servir a rien du tout. Merci d'avance

Le tableau est faux.
1 -2x/(2√(64-x²)) = 0 équivalent à
1 - x/√(64-x²) = 0 si on réduit au même dénominateur
[√(64-x²) - x]/√(64-x²) = 0
une fraction est nulle si son numérateur est nul et son dénominateur non nul soit
√(64-x²) - x = 0
ou x = ....

merci beaucoup c'est tout de suite beaucoup plus clair
bonne continuation !