Déterminer nature d'un quadrilatère et centre de gravité

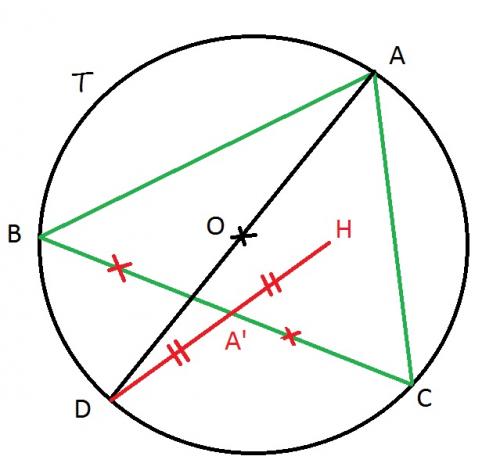
Bonjour, je suis en seconde et j'ai l'exercice 59 page 222 de transmath à faire (qui sera noté ) , or j'ai beaucoup de difficultés à le faire, pourriez-vous m'aider s'il vous plaît ? Voici l'énoncé ainsi que la figure :

T est le cercle de centre O circonscrit au triangle ABC. [AD] est un diamètre de T. H est le symétrique de D par rapport au milieu A' de [BC].

a) Quelle est la nature du quadrilatère BDCH ?

Ma réponse: Dans le quadrilatère BDCH : (BC) et (HD) qui sont les diagonales ont le même milieu donc BDCH est un parallélogramme. (est-ce la bonne réponse ? si oui, ai-je bien expliqué pourquoi ? svp )

b) Déduisez-en que (BH) est perpendiculaire à (AC) et que (CH) est perpendiculaire à (AB).

Je ne sais pas comment m'y prendre et quoi utiliser pour déduire cela

c) Que représente H pour le triangle ABC ?

H est le centre du cercle circonscrit donc le point d'intersection des médiatrices.

La droite (OH) coupe (AA') en G.
a) Démontrez que G est le centre de gravité du triangle ADH.

Le centre de gravité est l'intersection des médianes. Les médianes sont des droites qui joignent un sommet au milieu du côté opposé. Je nomme D' le point qui sépare (AH) en deux parties égaux. Donc (AA'), (DD') et (OH) sont des médianes et elles se coupent en G qui est donc le centre de gravité du triangle ADH.

b) Pourquoi AG = (2/3)*AA' ? Déduisez-en que G est aussi le centre de gravité du triangle ABC.

Merci d'avance ! $fichier math$

Bonsoir Unkoala,

Quelle est la nature des triangles ACD et ABD ?

Pourquoi les médiatrices ?

Ce sont des triangles rectangles,

je me suis trompée ce sont des hauteurs.

Oui,

Donc tu as trouvé les réponses aux questions b) et c) ?

b) (BH) est parallèle à (DC) dans le parallélogramme DCHB.
D et A étant diamètrement opposé alors l'angle DCA est droit donc DC est parallèle à AC.
Par suite BH parallèle à DC est perpendiculaire à AC.

c) (CH) est une hauteur issue de C et (BH) est une hauteur issue de B. Elles se coupent en H qui est donc leur point de concourt : l'orthocentre.

c'est ça ? :$

Attention c'est (DC) perpendiculaire à (AC) et non parallèle.
et plus de rigueur dans la démonstration.
(DC) perpendiculaire à (AC)
or
(DC) parallèle à (BH)
donc
(BH) perpendiculaire à (AC) car ..

J'ai trouvé... Merci