Trajet le plus cours (devoir maison)

Sujet: L'objectif est de déterminer où placer le pont [HK] perpendiculaire aux berges de la rivière, supposées parallèles, pour que la longueur du trajet de A à B soit la plus petite possible.

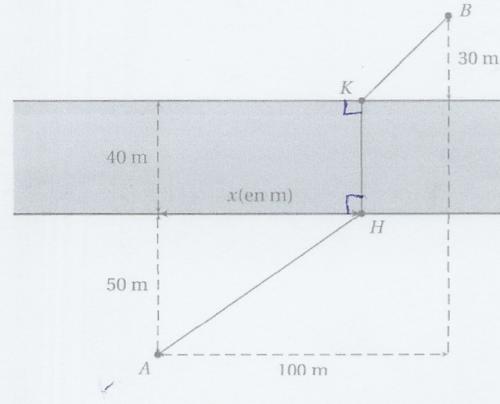
$fichier math$
Il y a deux façons de faire la première est surtout numérique. J'ai trouvé après plusieurs calculs que x doit être égale à 60m pour que le trajet soit le plus court.
Par contre pour la deuxième, l'exercice indique que la méthode est purement géométrique basée sur un réarrangement des trajets pour résoudre ce problème qui est accessible depuis la 4° (Théorème de Thalès nécessaire pour conclure).

Pour le théorème j'ai pensé à la configuration basique où il faudrait supprimer les 40m pour les calculs puis les rajouter à la fin. Mais j'ai beau revoir mes leçons de 4°, me creuser la tête je n'arrive pas à prouver la bonne solution.
Alors si quelqu'un peut au moins ne dire ce que je dois utiliser pour trouver la solution ce serait super !
Merci d'avance.

Bonsoir YoupiYoup,

Ton hypothèse est correcte, si on enlève la rivière,
les points A et B doivent être sur la même droite
donc tu retournes le triangle et tu as une configuration de Thalès.
Tu dois trouver x = 62,5 m.

D'accord merci.
Mais Thalès est nécessaire pour conclure et il me manque au moins une mesure pour l'utiliser. Quel(s) propriété(s) géométrique(s) dois-je utiliser pour pouvoir "être sur le chemin" de la solution ?

Quelle dimension il manque ?

Avec Thalés, tu peux calculer x.

Indique tes calculs.

D'après Thalès : 50/30 = AH/KB = x/K..
(produit en croix) x= 50*K../30
et après je peux plus avancer...

Comment je peux calculer avec Thalès ?

KI = 100 - x !

Ah mais ça fait :
x=(50*100-x)/30
x=(5000-x)/30
x=500/3-x/30
x≈167-x/30

Est ce que je peux faire ça:
x=167-x/30
x+x/30=167
2x=167/30
2x=6
x=6/2
x=3 (Mais ça correspond pas au résultat attendu...--')

50/30 = x/(100-x)
50(100-x) = 30x

Je te laisse poursuivre

C'est bon j'ai trouvée !
Merci beaucoup beaucoup beaucoup !!!

Bonjour, j'ai le même DM à faire et je n'ai pas compris tout ce qui a été expliqué ! Je souhaiterais qu'on me réexplique clairement si possible ! Merci !

Bonsoir,

cldouet14, c'est à YoupiYoup que Noemi à répondu.

Précise ta question si tu as besoin d'aide.

Je voudrais savoir comment il est possible d'utiliser Thalès en retirant la rivière ? Je n'arrive pas à me visualiser une configuration.

Bonsoir cidouet14,

Fais une figure en faisant glisser le triangle du dessus de façon à faire coïncider les points H et K.

Quelle figure obtiens tu ?