Problème de probabilités
-
SShizangen dernière édition par
Bonsoir je suis en train de faire mon problème qui concerne la probabilité,
Dans une région pétrolifère, la probabilité pour qu'un fourrage conduise à une nappe de pétrole est de 0,1.
- Justifier que la réalisation d'un forage peut être assimilé à une épreuve de Bernoulli.
2.On effectue 9 forages.
a. Quelle hypothèse doit-on faire pour que l'on puisse assimiler cet enchaînement de 9 épreuves à un schéma de Bernoulli ?
b. Sous cette hypothèse, calculer la probabilité:
- qu'au moins un forage conduise à une nappe de pétrole;
- qu'un tiers exactement des forages conduisent à une nappa de pétrole.
c. On désigne par X la variable aléatoire définie par le nombre de pétrole.
- Donner la loi de probabilité de X
- Combien de forages "gagnants" peut-on espérer en moyenne sur les 9 tentés ?
-
Evolution constante
-
a/ 9 * 0.1 = 0.9
- Justifier que la réalisation d'un forage peut être assimilé à une épreuve de Bernoulli.
-
Bonsoir Shizangen,
La première partie correspond au cours.
Epreuve de Bernoulli ?
Schéma de Bernoulli ?
Puis relation de Bernoulli ?
-
mtschoon dernière édition par

Bonjour Noemi et Shizangen,
Shizangen, commence bien sûr , comme te le conseille Noemi , par utiliser ton cours.
Quelques pistes pour poursuivre,
Sur un forage ( une "épreuve" ) ,la probabilité d'un succès( pour qu'un forage conduise à une nappe de pétrole ) est de 0,1 :p=0.1
La probabilité d'un échec est 1-p=0.9
9 forages : 9 épreuves répétées indépendantes.
Soit X le nombre de succèsLa probabilité de k succès est :
$\fbox{p(x=k)={{9\choose {k}}p^k(1-p)^{9-k}={{9\choose k}}0.1^k0.9^{9-k}}$ (***)*La probabilité qu'au moins un forage conduise à une nappe de pétrole est p(X ≥ 1)
Je te conseille de passer par l'évènement contraire :
p(x≥1)=1−p(x=0)p(x \ge 1)=1-p(x=0)p(x≥1)=1−p(x=0)
Tu remplaces k par 0 dans la formule () et tu comptesLa probabilité qu'un tiers exactement des forages conduise à une nappe de pétrole est p(x=3)p(x=3)p(x=3) vu que (1/3) x 9=3
Tu remplaces k par 3 dans la formule () et tu comptesPour la loi de probabilité*, dispose les résultats ( formule (***)) sont forme de tableau , en faisant varier k de 0 à 9(Remarque : lorsque tu auras fait tous les calculs , assure toi que la somme des probabilités vaut bien 1 )
Pour la moyenne , utilise la formule de ton cours relative à l'espérance mathématique .
Bon travail.
-
SShizangen dernière édition par
Salut,
- Un schéma de Bernoulli d’ordre n est la répétition d’une épreuve de Bernoulli n fois où chaque issue est indépendante.
a/ 9 forages = 9 épreuves répétées indépendantes.
b/ je suis en train de le faire.
-
mtschoon dernière édition par

Bons calculs !
-
SShizangen dernière édition par
J'ai une question. Le (9 k) mais vertical comme tu l'as fait dans ta formule c'est une division ? Dois je comprendre que c'est 9/k ou (9;k)?
-
mtschoon dernière édition par

(9k){{9}\choose {k}}(k9) est le nombre de combinaisons de k éléments choisis parmi 9 .
J'ignore comment c'est écrit dans ton cours , mais c'est la notation usuelle .
L'ancienne notation était c9kc^k_9c9k
Un exemple :
(92)=9×82×1=36{{9}\choose {2}}=\frac{9\times 8}{2\times 1}=36(29)=2×19×8=36
Tu dois trouver les combinaisons sur ta calculette.
Sur la mienne , c'est la fonction nCr : nCr(9,2) me renvoit 36 , mais toutes les calculettes n'ont pas la même syntaxe...
-
SShizangen dernière édition par
Sur ma calculette (9,0) = 1
Mais sur la formule j'ai gardé quand même (9,0) et pas 1:

-
SShizangen dernière édition par
Pardon je me suis trompé au premier c'est pas (9,2) que je voulais marquer mais bien (9,0)p^0.
-
mtschoon dernière édition par

Vu que :
(90)=1{{9}\choose {0} }=1(09)=1
p0=1p^0=1p0=1
tu obtiens :p(x=0)=0.99p(x=0)=0.9^9p(x=0)=0.99
( ceci est normal ,car dans ce cas il y a 9 échecs avec chacun la probabilité 0.9 )
-
SShizangen dernière édition par
Euh P(X=0)=0,9⁹ ? alors j'ai du me tromper dans la formule parce que j'ai fait
La probabilité qu'au moins un forage conduise à une nappe de pétrole est p(X ≥ 1)
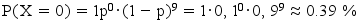
-
SShizangen dernière édition par
Ah non c'est bon je dis n'importe quoi c'est le même résultat ^^ je suis bidon.
La probabilité qu'un tiers exactement des forages conduise à une nappe de pétrole P(X=3)(puisque 1/3*9=3)
9C3 = 84 et p^84 = 1
-
mtschoon dernière édition par

oui pour le "84" mais que fait ce "p^84=1" ?
$p(x=3)={{9\choose {3}}p^3(1-p)^{9-3}$
-
SShizangen dernière édition par

-
mtschoon dernière édition par

Tu mélanges les notations.
p(x=3)=84×0.13×(1−0.1)9−3p(x=3)=84 \times 0.1^3 \times (1-0.1)^{9-3}p(x=3)=84×0.13×(1−0.1)9−3
p(x=3)=84×0.13×(0.9)6p(x=3)=84 \times 0.1^3 \times (0.9)^{6}p(x=3)=84×0.13×(0.9)6
-
SShizangen dernière édition par
= s oula.
 %
%
-
mtschoon dernière édition par

C'est bon pour P(X=3)
Remarque : Pour ta première question , tu as calculé P(X=0) , mais j'espère que tu n'as oublié de calculer1-P(X=0)