Etudier une fonction et donner son tableau de variations

[melimelo00]

Bonjour,
Je dois rendre un exercice sur l'étude d'une fonction .
Voici l'énoncé:
Soit∅ :x→x²/(x-1) et C sa courbe représentative dans un repère orthogonal du plan.

1- Indiquer l'ensemble de définition, noté E dans la suite de l'exercice, de∅ .
2- Déterminer trois réels a,b et c tels que, pour tout réel x appartenant à E ,∅(x)=ax+b+c/(x-1)
3- Expliquer de manière claire et concise pourquoi l'écriture de ∅(x) obtenue à la question précédente n'est d'aucun secours pour déterminer aisément les variations de .
4- Démontrer que C admet un centre de symétrie dont on précisera les coordonnées.
5- On admet que le tableau de variations de ]1;+∞[ est le suivant: (voir en dessous)
A l'aide de la calculatrice graphique , conjecturer la valeur m de x en laquelle ∅ atteint son minimum sur ]1;+∞[ puis valider cette conjecture en vérifiant que, pour tout x appartenant à ]1;+∞[, la différence (∅(x)-(∅m)) est positive.
6-En déduire
a) les variations de ∅ sur]-∞;1[
b) les variations de f:x→(x-1)/x² sur ]1;+∞[
c) les variations de g:x→x/(x-1) sur ]1;+∞[

J'ai commencé l'exercice et pense à voir réussi les questions 1 et 2

1. l'ensemble de définition est $mathbbR$ -{1}
2. je trouve a=1 b=1 et c=1
   J'aimerai avoir une confirmation des ces réponses pour savoir si mes résultats sont corrects et avoir de l'aide pour la suite .Merci d'avance .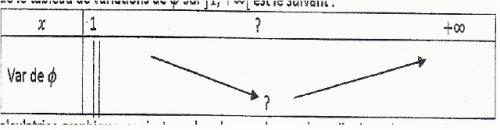

[Noemi]

Bonjour melimelo00,

le début est juste.
3 comment on étudie les variations d'une fonction ?
4 comment détermine t-on un centre de symétrie ?

[melimelo00]

d'accord merci .
3) On obtient ainsi l'écriture x + 1 + 1/(x-1)

Or x + 1 est une fonction croissante , et 1/(x-1) est une fonction décroissante ( inverse d'une fonction croissante )

On ne peut pas conclure sur le sens de variation de la somme d'une fonction croissante et d'une fonction décroissante c'est bien ça ?

4. Pour démontrer la présence de l'axe de symétrie :Est ce que dire que que x² est une fonction carré et qu'elle a pour représentation graphique une parabole est suffisent comme justification ?

[Noemi]

Connais tu la propriété :
Si le point S(x1;y1) est centre de symétrie, f(x1-x) + f(x1+x) = 2y1 ?

[melimelo00]

oui je la connais donc du coup maintenant que je sais l'utiliser j'ai pu répondre à la question .. Merci beaucoup

j'ai réussi à continuer l'exercice mais la question 6) me pose problème
b) je sais que f est l'inverse de la fonction ∅; et j'ai repris mon cours pour retrouver les variations de la fonction inverse mais j'ai du mal à mettre ma réponse sous forme de tableau de variation est ce qu'il y a une valeur interdite ?
c) et c'est la même chose pour cette question je m'embrouille avec les sens de variation et l'intervalle et je ne sais pas si il faut mettre une valeur interdite..

[melimelo00]

oui je la connais donc du coup maintenant que je sais l'utiliser j'ai pu répondre à la question .. Merci beaucoup

j'ai réussi à continuer l'exercice mais la question 6) me pose problème
b) je sais que f est l'inverse de la fonction ∅; et j'ai repris mon cours pour retrouver les variations de la fonction inverse mais j'ai du mal à mettre ma réponse sous forme de tableau de variation est ce qu'il y a une valeur interdite ?
c) et c'est la même chose pour cette question je m'embrouille avec les sens de variation et l'intervalle et je ne sais pas si il faut mettre une valeur interdite..

[melimelo00]

oui je la connais donc du coup maintenant que je sais l'utiliser j'ai pu répondre à la question .. Merci beaucoup

j'ai réussi à continuer l'exercice mais la question 6) me pose problème
b) je sais que f est l'inverse de la fonction ∅; et j'ai repris mon cours pour retrouver les variations de la fonction inverse mais j'ai du mal à mettre ma réponse sous forme de tableau de variation est ce qu'il y a une valeur interdite ?
c) et c'est la même chose pour cette question je m'embrouille avec les sens de variation et l'intervalle et je ne sais pas si il faut mettre une valeur interdite..

[melimelo00]

oui je la connais donc du coup maintenant que je sais l'utiliser j'ai pu répondre à la question .. Merci beaucoup

j'ai réussi à continuer l'exercice mais la question 6) me pose problème
b) je sais que f est l'inverse de la fonction ∅; et j'ai repris mon cours pour retrouver les variations de la fonction inverse mais j'ai du mal à mettre ma réponse sous forme de tableau de variation est ce qu'il y a une valeur interdite ?
c) et c'est la même chose pour cette question je m'embrouille avec les sens de variation et l'intervalle et je ne sais pas si il faut mettre une valeur interdite..

[melimelo00]

oui je la connais donc du coup maintenant que je sais l'utiliser j'ai pu répondre à la question .. Merci beaucoup

j'ai réussi à continuer l'exercice mais la question 6) me pose problème
b) je sais que f est l'inverse de la fonction ∅; et j'ai repris mon cours pour retrouver les variations de la fonction inverse mais j'ai du mal à mettre ma réponse sous forme de tableau de variation est ce qu'il y a une valeur interdite ?
c) et c'est la même chose pour cette question je m'embrouille avec les sens de variation et l'intervalle et je ne sais pas si il faut mettre une valeur interdite..

[melimelo00]

je m'excuse pour la répétition du mon message mon ordinateur a eu un petit problème et je ne sais pas comment supprimer les messages répétés ..

[Noemi]

Pour la question 6,
a) tu utilises le fait que la fonction admet un centre de symétrie.

[melimelo00]

D'accord merci beaucoup j'ai réussi à terminer mon exercice.