Problème sur les primitives : intégrales indéfinies (substitution)

Bonsoir (ou bonjour, ça dépend) à tous et à toutes !

Comme j'entre en période d'examens, le prof de math nous a donné quelques exercices et je cale sur 7 des 20 exercices sur les intégrales indéfinies ( technique de substitution)
Quelqu'un pourrait-t'il me donner une piste pour résoudre ces équations? Je cale dessus depuis 3 jours, et n'ayant pas eu cours de math depuis 2 semaines (avec un prof absent ... ) je n'ai pas eu l'occasion de lui demander de l'aide ! :s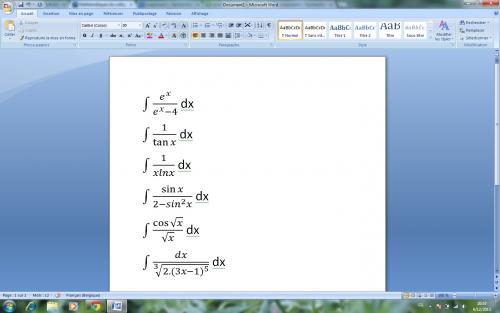

Exercices sur les intégrales indéfinies

Merci d'avance !

Bonsoir Dulcianna,

Indique tes éléments de réponse.

Pour la première c'est de la forme u'/u

Je n'ai justement pas d'éléments de réponse excepté quelques formules comme les formules de bases pour les primitives et la formule de substitution de dx = du / u'

Je ne sais pas si c'est ça que tu veux dire par "éléments" de réponse?

Indique tes calculs,
si u(x) = $e^x$ -4,
u'(x) =

hum
J'ai commencé par:

u= e^x-4
u'= e^x

Ensuite, j'ai dx = du/ e^x

--> ]e^x / u . du/ e^x
On simplifie

Et je tombe sur ]1/u . du =
] 1/ e^x-4 . du= ln (e^x-4) + c

] représente le signe de l'intégrale. Mais je ne suis pas sure du raisonnement ...

C'est correct,

applique le même raisonnement pour les autres;
tan x = sinx/ cosx
....