Problème avec etude de fonction
-
Ccoshy95 dernière édition par
Un charpentier a tracé à main levé le profil d'un étage sous les toits laissant libre un espace rectangulaire OABC. Il souhaite étudier la hauteur h en fonction de la largeur du sol x. Sur son schéma, les longueurs sont exprimées en mètres.
On appelle f la fonction qui à x associe la hauteur h.J'ai mis l'image du schéma avec le post.
Question : Montrer que f(x) = 2 + 6/x-3
Donc f(x) = 2 + AD.
Ensuite je ne sais quoi faire ...
Pourriez-vous m'éclairer ? Svp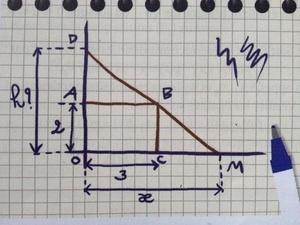 }
}
-
Bonsoir coshy95,
Applique la propriété de Thalès aux triangles DAB et DOM
-
Ccoshy95 dernière édition par
Ah merci donc ca me donne ca : AB/OM = BC/DO = ....
Je trouves pas la 3eme relation.
-
Ccoshy95 dernière édition par
Ce serait pas plûtot ca : AB/OM = DA/DO = DB/DM. ?
-
C'est
AB/OM = DA/DO = DB/DM
-
Ccoshy95 dernière édition par
Mercii j'étais en train de rectifier le post xD merci
-
Ccoshy95 dernière édition par
Je connais que AB et OM ca fait que je suis bloqué pour faire la relation de thales :
3/x = DA/DO = DB/DM
-
Ccoshy95 dernière édition par
Et du coup comment je démontre que f(x) = 2 + 6/x-3 ?
-
DA = h-2 et DO = h
-
Ccoshy95 dernière édition par
Ouii ca me donne h-2/h = 3/x
Et du coup que dois-je faire ?
-
Isole h,
h = ..... (en fonction de x)
-
Ccoshy95 dernière édition par
Toujours pas compris... Désolé
-
h-2/h = 3/x
(h-2)x = 3h
hx - 3h = 2x
h(x-3) = 2x
h = ...
-
Ccoshy95 dernière édition par
h = 2x/x-3 ?
Mais je comprends pas pourquoi je fais ca car j'obtiens paq l'expression qu'il me dise dans la quesion que je dois prouver.
-
Ccoshy95 dernière édition par
h = 2x/x-3 ?
Mais je comprends pas pourquoi je fais ca car j'obtiens paq l'expression qu'il me dise dans la quesion que je dois prouver.
-
C'est la relation demandée, il reste une transformation à faire
h = 2x/(x-3)
h = (2x-6+6)/(x-3)
h = (2x-6)/(x-3) + 6/(x-3)
h = 2(x-3)/(x-3) + 6/(x-3)
h = ....
-
Ccoshy95 dernière édition par
Pas compris... Mais merci beaucoup j'ai trouvé la réponse quelqu'un l'avait déjà fait ici : http://www.ilemaths.net/forum-sujet-453783.html