DM limite et logarithme népérien
-
SShizangen dernière édition par
Bonjour j'ai un devoir maison à éffectuer et j'aimerais un pe u d'aide:
Partie A
On se propose d'étudier la fonction f définie sur l'intérvalle ]0,+∞[ par:

- On définit la fonction g sur l'intervalle ]1;+∞[ par:

a) Quelle est la limite de g en 1 ?
b) Calculer g'(x) pour x appartenant à l'intervalle ]1;+∞[
c) Résoudre dans l'intervalle ]1;+∞[ l'inéquation:
d) Etudier le sens de variation de g sur l'intervalle ]1;+∞[.
e) Démontrer que l'équation g(x) = 0 a une solution unique, notée α, dans l'intervalle [e+1;e³+1] et étudier le signe de g(x) sur chacun des intervalles ]1;α[ et]α;+∞[.- φ est la fonction définie sur l'intervalle ]1;+∞[ par:
d) Etudier le sens de variation de g sur l'intervalle ]1;+∞[.
e) Démontrer que l'équation g(x) = 0 a une solution unique, notée α, dans l'intervalle [e+1;e³+1] et étudier le signe de g(x) sur chacun des intervalles ]1;α[ et]α;+∞[.- φ est la fonction définie sur l'intervalle ]1;+∞[ par:

a) Etudier la limite de la fonction φ en 1;
On admet que φ admet pour limite 0 en +∞.
b) Déterminer φ' (x)
Démontrer que φ' (x) est du signe de g(x²) sur l'intervalle ]1;+∞[.
c) Démontrer que φ est croissante sur l'intervalle ]1;√α[ et décroissante sur l'intervalle ]√α;+∞[Partie B
- Vérifier que pour tout x de 'lintervalle ]0;+∞[ :

- En déduire:
a) la limite de f en 0;
b) la limite de f en +∞
c) le sens de variation de f sur l'intervalle ]0;+∞[ et que f admet un maximum en ln(√α). - Montrer que pour tout x de l'intervalle ]0;+∞[ :

- Reproduire le tableau suivant et le compléter en donnant les arrondis au centième.

- Représenter graphiquement f dans un repère orthopgonal, d'unité 5 cm en abscisses et 10 cmen ordonnées. On prendra 10 comme valeur approchée de α.
Réponses:
a) g(1) = 2 -0Ln(0)
g(1) → 2
-
mtschoon dernière édition par

Bonjour,
Fais attention ! ln0 n'existe pas !
Condition d'existence de g : x-1 > 0 <=> x > 1
dg=]1,+∞[dg=]1,+\infty[dg=]1,+∞[
Lorsque x tend vers 1+1^+1+ , (x-1) tend vers 0+0^+0+
Tu dois savoir que limx→0+xlnx=0\lim_{x\to 0^+}xlnx=0limx→0+xlnx=0
Donc : limx→1+(x−1)ln(x−1)=0\lim_{x\to 1^+}(x-1)ln(x-1)=0limx→1+(x−1)ln(x−1)=0
Donc : limx→1+g(x)=....\lim_{x\to 1^+}g(x)=....limx→1+g(x)=....
-
SShizangen dernière édition par
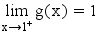
-
mtschoon dernière édition par

non...
-
SShizangen dernière édition par

b.

A partir de la 3 ème ligne j'ai essayé d'appliquer la dérivé d'un produit pour (x-1)Ln(x-1)
-
mtschoon dernière édition par

Essaie de comprendre la limite en 1 : c'est tout simple.
limx→1+(x−1)ln(x−1)=0\lim_{x\to 1^+}(x-1)ln(x-1)=0limx→1+(x−1)ln(x−1)=0
Il reste à trouver la limite de 2x , lorsque x tend vers 1 .
Lorsque x tend vers 1, 2x tend vers ...
donc
limx→1+g(x)=....−0=...\lim_{x\to 1^+}g(x)=.... -0 =...limx→1+g(x)=....−0=...
- Fais attention car il y a une différence.
g′(x)=2−[(x−1)ln(x−1)]′g'(x)=2-[(x-1)ln(x-1)]'g′(x)=2−[(x−1)ln(x−1)]′
En prenant la dérivée du produit que tu as faite , après simplification ; tu dois trouver
g′(x)=1−ln(x−1)g'(x)=1-ln(x-1)g′(x)=1−ln(x−1)