Probabilités et intervalle de fluctuation
-
Cchat dernière édition par
Bonjour,
Exercice :
Un journaliste écrit :
"Seulement 65% des ménages vivant à Paris possèdent une voiture".
On consulte la situation de 50 ménages parisiens choisis au hasard et on note X la variable aléatoire associée au nombre de ménages possédant un véhicule, parmi les 50. On admet que la variable aléatoire X suit la loi binomiale B (50 ; 0,65).- Donner la formule à saisir en cellule B2, et à recopier vers le bas, pour obtenir les probabilités P(X ≤ k) du tableau suivant.
Voir pièce jointe :
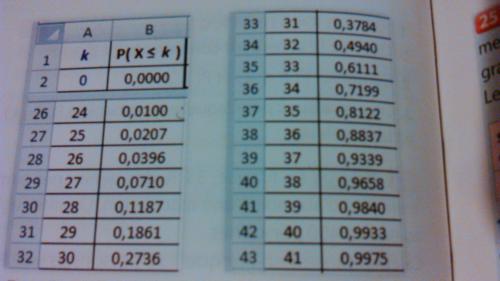
- En utilisant les extraits de table, déterminer :
P(X ≤ 30), P(X ≤ 33) et P (X > 36).
- a) Lire sur la table le plus petit entier a tel que :
P(X ≤ a) > 0,025
et le plus petit entier b tel que P(X ≤ b) ≥ 0,975.
b) En déduire l'intervalle [a/n ; b/n], intervalle de fluctuation à 95% de la fréquence.
- En réalité, sur les 50 ménages considérés, 37 ménages possèdent une voiture.
Peut-on rejeter l'affirmation du journaliste ?
Voici mes réponses :
-
=LOI.BINOMIALE(A2;50;0,65;VRAI)
-
P(X≤30) ≃ 0,2736
P(X≤33) ≃ 0,6111
P(X>36) = 1 - P(X ≤ 36)
= 1 - 0,8837
= 0,1163 -
a)
P(X≤26) ≃ 0,0396 > 0,025
a = 26
P(X≤39) ≃ 0,9840 ≥ 0,975
b = 39
Intervalle de fluctuation à 95% :
[a/n;b/n] soit [26/50;39/50] = [0,52;0,78]
f = 37/50 = 0,74
f ∈ [0,52;0,78]
On ne rejette donc pas OU On accepte donc l'affirmation du journaliste au risque 5%.
(Je ne sais pas trop comment bien formuler cette phrase).Pouvez-vous m'aider et me dire mes erreurs, ce qui n'est pas bon dans mes calculs, si mes réponses sont bonnes, si c'est bien rédigée... s'il vous plait. Merci d'avance.
edit : merci de donner des titres significatifs
-
mtschoon dernière édition par

Bonjour,
Je viens de vérifier tes réponses : tout est bon.
Pour l'explication de l'intervalle de fluctuation à 95%, tout dépend de ce que te dit ton cours.
De façon générale, cet intervalle est
i=[p−1n,p−1n]i=[p-\frac{1}{\sqrt n},p-\frac{1}{\sqrt n}]i=[p−n1,p−n1]
pour n ≥ 25 et 0.2 ≤ p ≤ 0.8 (Ici, n=50 et p=0.65)
Pour une loi binomiale, on choisit l'intervalle
j=[an,bn]j=[\frac{a}{n},\frac{b}{n}]j=[na,nb] (que l'énoncé te demande de calculer).
Cet intervalle J est sensiblement le même que I.
Si cette explication est donnée dans ton cours, tu n'as rien à justifier; sinon, tu expliques.
Pour la dernière phrase, tu peux peut-être dire que, au seuil de 5%, l'affirmation du journaliste est vraie.