Démontrer qu'une droite est orthogonale à un plan

Bonjour, j'ai un exercice à faire mais je ne comprends pas du tout.. J'aurais besoin d'aide.. Merci d'avance !

SABCD est une pyramide dont la base ABCD est un carré de côté 6 et telle que les faces ABS et ADS sont des triangles isocèles en A. On définit les points I et J comme étant les milieux respectifs de [SB] et [SC].

Faire une figure en perspective cavalière représentant la situation, et représenter le quadrilatère AIJD en couleur.
Démontrer que A, I, J, D sont coplanaires.
Démontrer que la droite (AD) est orthogonale à (ABS).
En déduire que les droites (IJ) et (AI° sont orthogonales.
Déterminer précisément la nature du quadrilatère AIJD, puis calculer son aire.
Démontrer que la droite (SI) est orthogonale au plan (AIJ).
En déduire le volume de la pyramide SAIJD.
Calculer le volume de la pyramide SABCD, puis en déduire celui du solide AIBDJC.

Merci encore à ceux qui me répondront, LILI70

Bonjour,

Pour t'éclairer un peu, j'ai tenté de te faire un schéma.

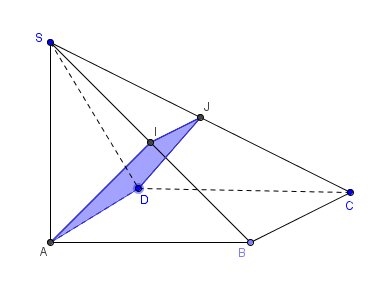
$fichier math$

Si besoin, tiens nous au courant de tes réponses

Merci pour la figure voici ma réponse à la question 2.

AD= coté du carré ABCD
I milieu de BS
J milieu de CS
[BC] est un coté de ABCD
(IJ) est donc parallèle à (BC)
(BC)//(AD) car appartiennent à ABCD
donc (IJ)//(AD)
2 droites étant // sont coplanaires
Donc (IJ) et (AD) sont coplanaires
ainsi A, I, J, et D sont coplanaires

J'ai commencé la question 3, mais je bloque:

ABS est un triangle rectangle et isocèle en A
AD est un coté du carré ABCD
(AD) perpendiculaire à (AB) (( carré ABCD))

voilà !
LILI70

Effectivement, vu l'énoncé écrit, il est normal que tu bloques à la 3)...

N'aurais-tu pas oublié une donnée de l'énoncé ?

Tu as écrit :

Citation
ABS et ADS sont des triangles isocèles en A.

Dans l'énoncé original, n'y aurait-il pas écrit :ABS et ADS sont des triangles isocèles etrectangles en A ?

Ah oui effectivement.. C'est bien bien des triangles isocèles rectangles en A

Je m'en doutais un peu...c'est ce que j'ai essayé de représenter sur la graphique

Piste pour la 3) (à expliciter)

(AD) ⊥ (AB) et (AD) ⊥ (AS) => (AD) ⊥ plan(ABS)

(rappel : une droite est perpendiculaire à un plan si et seulement si elle est orthogonale à deux droites concourantes de ce plan)

d'accord je vois.. merci

comment puis-je calculer la longueur IJ ?

J'ai trouver IJ=3 cm, moitié de BC par théoreme de thalès

comment montrer que SI est orthogonale à (AIJ) ?

Tu dois trouver deux droites concourantes du plan (AIJ) orthogonales à (SI)

Pistes,

Le triangle SBC est rectangle en B (car l'angle $abc^\widehat{abc}$ est droit)

Donc : (SB) ⊥(BC)

Or (IJ) // (BC)

Donc (SI) ⊥ (IJ)

D'autre part, le triangle SAB étant isocèle rectangle, la médiane (AI) est aussi hauteur,

donc (AI) ⊥(SI)

Tu peux tirer la conclusion souhaitée.

d'accord j'ai compris merci

pour AIJD j'ai trouvé un trapèze rectangle en I, d'aire 19,035cm²

est-ce que cela doit me servir pour les questions 7 et 8 ?

Pour l'aire AIJD , donne tes calculs si tu veux une vérification.
En plus , la valeur doit être irrationnelle plutôt qu'une valeur approchée.

Oui cette aire servira aux dernières questions.

Rappel :

$\text{aire(pyramide)=\frac{1}{3} \times aire(base) \times\ hauteur$

AI=4,23cm (par théoreme de pythagore)
DJ=4,23cm
IJ= 3cm (moitié de BC par théorème de thalès)

Aire= (petite base + grande base)*hauteur /2
= (3+6)*4,23 /2
= 19,035 cm²

je ne sais pas quoi prendre comme hauteur pour la pyramide SAIJD

pour SABCD :

Aire(SABCD)= 1/3 * 6*6 * 6 =72cm²

est-ce bon ?

Comme je te l'ai déjà indiqué, mets les valeurs irrationnelles exactes ( non les valeurs approchées de ta calculette)

$3\sqrt 2$

donc...

Pour la pryramide, relis les questions précédentes et tu sauras quelle est la hauteur.

en prenant AI= 3√2 on a aire=19,09 cm²

la hauteur serait SI ?

Cela fait maintenant la 3ème fois que je te le dis...
Donne la valeur exacte et non approchée de l'aire ( valeur avec √2)

Oui la hauteur est (SI)

D'accord, je vais mettre ça en valeur exacte

Merci beaucoup pour votre aide !

LILI70

De rien.

J'espère que tu vas répondre

$\text{ aire(aijd)=\frac{27\sqrt 2}{2}$

Tu auras ainsi facilement le volume de la pyramide (SAIJD)

En calculant ensuite le volume de la pyramide (SABCD), puis en faisant la différence des 2 volumes, tu obtiendras le dernier volume demandé.

Bon travail !